有限样本学习（三）：数据生成

翻译自：Learning with not Enough Data Part 3: Data Generation，谢谢 Lilian Weng的分享。

简介：这是有限样本学习的第三方部分内容（第一部分/第二部分）。我们考虑两种生成训练数据的方法：

1. 数据增强：给定现有的训练样本集合，我们应用一系列数据增强、修改和变换方法来派生出新的数据，并且让新生成的数据不丢失关键信息。在前面对比学习的文章中，我们已经介绍了一些文本和图片增强的方法。为了内容的完整性，此篇文章使用了一小节内容来介绍那些方法
2. 新数据：给定极少量或没有数据，我们可以依赖于预训练模型来生成新的数据点。鉴于近年来预训练语言模型（Language Model, LM）快速发展，此方法的可行性大大增加。在上下文学习中，few shot prompting在无须额外训练的情况下已展示出有效性

数据增强

数据增强的目标是在保持原本数据语义不变的情况下，修改输入的格式（比如：文本单词、视觉效果等）来生成新的数据。

图片增强

基础图片处理操作

在保持语义的情况下，有很多方法来修改一张图片。我们可以使用下面的方法中的一种或几种的混合：

• 随机裁剪然后缩放到原有大小
• 随机颜色混合
• 随机高斯模糊（Gaussian blur）
• 随机颜色抖动
• 随机水平翻转
• 随机灰度变换
• 其它：参考PIL.ImageOps

任务相关增强策略

如果下游任务是已知的，那么我们可以使用一些对下游任务性能提升有效的一些优化方法（也就是挑选合适的增强操作及其组合）。

• 自动增强（Cubuk 等, 2018）受神经架构搜索的启发，它将学习挑选最优数据增强操作（修建、旋转、翻转等）的过程建模为一个强化学习问题，寻找可以在评估集上达到最优准确率的操作组合。自动增强可以使用敌对形式（adversarial fashion）来进行（Zhang 等人, 2019）
• 随机增强（Cubuk 等, 2019）用一个控制不同变换操作规模的规模参数，大大降低了自动增强方法的搜索空间
• 种群增强（Population Based Augmentation, PBA;Ho 等, 2019）将PBT（Pupulation Based Training;Jaderberg 等 2017）与自动增强相结合，并行训练“一群”子模型来进化出最优的增强策略
• 无监督数据增强（Unsupervised Data Augmentation, UDA;Xie deng, 2019）在一个可行增强策略集中选择可以最小化一个KL散度的子集，此KL散度用于衡量在无标签样本上得到的一个分布估计与其对应增强版数据上的估计之间的相似度

图片混合

图片混合使用如下方法对现有数据进行合成：

• Mixup（Zhang 等, 2018）方法通过对两张图片$I_1, I_2$进行像素级整体合成：$I_{mixup} \leftarrow \alpha I_1 + (1-\alpha)I_2$,$\alpha \in [0, 1]$
• Cutmix（Yun 等, 2019）方法对两张图片进行区域级合成：从一张图片中取一部分，剩余部分取自另一部分，$I_{cutmix} \leftarrow M_b \odot I_1 + (1 - M_b) \odot I_2$, 其中$M_b \in \{ 0, 1 \}^I$为掩码，$\odot$为按元素乘操作。这和使用一张图片中对应部分填充另一张图片挖去（DeVries & Taylor, 2017）部分的方法一样
• 给定一个查询$\mathbf{q}$，MoChi（Mixing of Contrastive Hard Negatives; Kalantidis 等,2020）维护了一个包含$K$个负特征的队列$Q=\mathbf{n}_1, \ldots, \mathbf{n}_K$，并将这些负特征根据其与查询$\mathbf{q}$之间相似度进行降序排序。队列中前$N$个元素被认为是最硬的负特征$Q^N$。而后合成的硬样本可以通过公式$ \mathbf{h}=\tilde{\mathbf{h}}/|\tilde{\mathbf{h}}|_2\ $来合成，其中$\tilde{\mathbf{h}} = \alpha\mathbf{n}_i + (1-\alpha) \mathbf{n}_j$,$\alpha \in (0, 1)$。此外，更加硬核的样本可以通过将查询$\mathbf{q}$与特征进行混合得到：$\mathbf{h}' = \tilde{\mathbf{h}'} / |\tilde{\mathbf{h}'}|_2$，其中$\tilde{\mathbf{h}'} = \beta\mathbf{q} + (1-\beta) \mathbf{n}_j$,$\beta \in (0, 0.5)$

文本增强

词法编辑（Lexical Edits）

简易数据合成（Easy Data Augmentation, EDA; Wei & Zou, 2019）为文本增强定义了一系列简单而强大的操作。给定一个句子，EDA随机选择并应用下面四个操作中的一个：

1. 同义词替换：使用同义词随机替换$n$个非停用词
2. 随机插入：从一个句子中随机选择一个停用词，选择该词的一个同义词插入到句子中的一个随机位置
3. 随机替换：随机交换句子中的两个词，重复$n$次
4. 随机删除：以概率$p$随机删除句子中的每个词

其中$p=\alpha$,$n = \alpha \times len(\mathbf{sentence})$，从直觉上来看，更长的句子可以吸收更多的噪声而保持句子语义。超参数$\alpha$大致可以看作是一次增强操作中句子被修改词语所占的百分比。

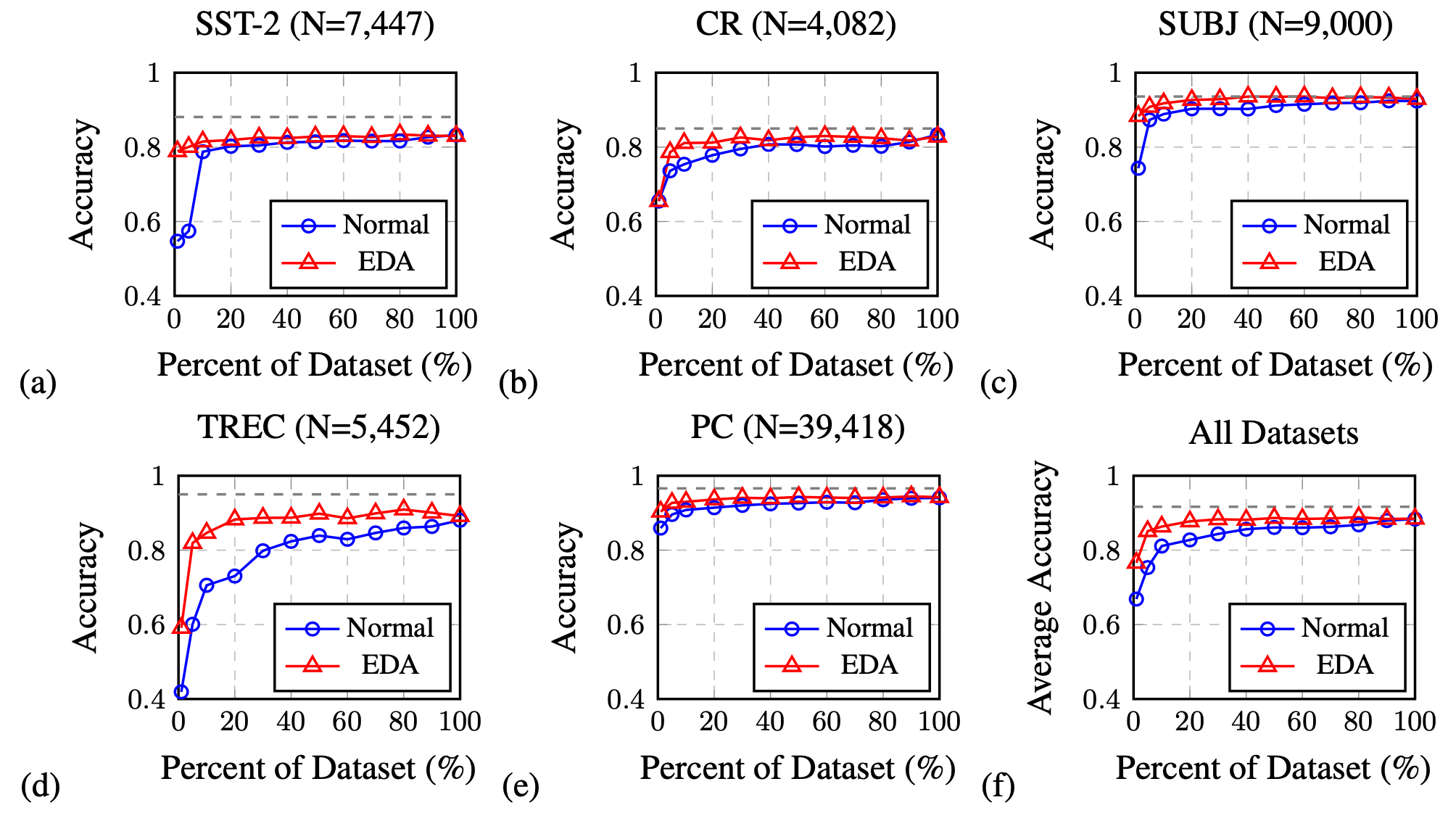
实验显示，EDA在一些分类基线数据集上可以改善准确率。性能提升在更小的训练集上更加显著。以上所有四个操作都可以改善分类准确率，但是它们最优的$\alpha$取值不同。

上下文增强（Kobayashi, 2018）将位置$i$处的词$w_i$替换为另外一个词$w_i^\prime$，$w_i^\prime$从一个类似BERT的双向语言模型学习到的概率分布$p(.\mid S\setminus{w_i})$中采样得到。通过此种方式，句子中的单词被替换为同义词或者与原词上下文相符的词。为了保证此操作不会改变标签，LM是一个基于标签的条件双向语言模型。CBERT（Contitional BERT;Xing Wu 等, 2018）对BERT进行扩展，它以样本标签为条件来预测被掩码掩去的词，可以被用作上下文增强中的预测模型。

回译（Back-translation）

回译将文本翻译成另外一种语言，再将译文翻译回原语言来得到增强后的数据。为了保证重要的语义不会丢失，两种翻译方式需要有足够的性能保证。

混合（Mix-up）

我们也可以将混合（Mix-up）操作应用到文本上（Guo 等, 2019），但此操作是应用在嵌入空间（embedding space）上的。所提方法依赖于一个特殊设计的模型来操作词/句子的嵌入。通过在嵌入空间中引入敌对噪声（adversarial noise）来作为数据增强的方法可以改善训练模型的范化性（Zhu 等, 2019）。

语音增强

Wang & van deng Oord, 2021总结了一些在原始语音或者声谱上的增强操作。

• 语音混合：给定两个语义片段$\mathbf{x}_1, \mathbf{x}_2$，那么混合版样本为$\hat{\mathbf{x}} = \alpha \mathbf{x}_1 + (1-\alpha)\mathbf{x}_2$，$\hat{\mathbf{x}}$应该与主要输入的标签相关。在语音混合增强中，我们可以使用现实的噪声
• 时间掩码：在一串语音中，将其中的一小段掩去（masked）
• 频率掩码：频谱中一小段频率可以被掩去
• 频率平移：频谱移动一个$[-F, F]$之间的整数值，其中$F$为最大偏移大小。改变音频的音高是一种廉价的增强方式

架构增强

模型的dropout层可以通过在同一个输入样本上应用不同的dropout掩码来生成增强样本。举例来说，在对比学习模型SimCSE（Guo 等, 2021）中，一个样本被简单喂入到编码器两次并应用两个不同的dropout掩码，这两个生成的噪声版被作为正样本，同一批（batch）数据中其它样本被用作负样本。

Dropout可以通过在模型内部隐层表示上添加噪声来进行数据增强。它可以以一种更加结构化的方式来被应用，比如cutoff（Shen 等, 2020），在此方法中，token的嵌入表示被随机去掉了几块（chunks）。

数据合成

生成高质量、照片级的图片要比生成自然语言文本困难得多。本节仅考虑文本生成。想要了解如何合成接近真实的图片，可以参考GAN,VAE,flow和diffusion模型。

语言模型作为噪声注释器

Wang 等, 2021应用小样本提示（few-shot prompting）探索了将GPT-3来作为弱注释器的方法，此方法相比人工标记便宜了10倍。论文认为使用GPT-3标记数据本质上是进行自训练（self-training）：在无标签样本的预测上应用熵正则化来避免过高的类别重合度，可以帮助改善模型的性能。

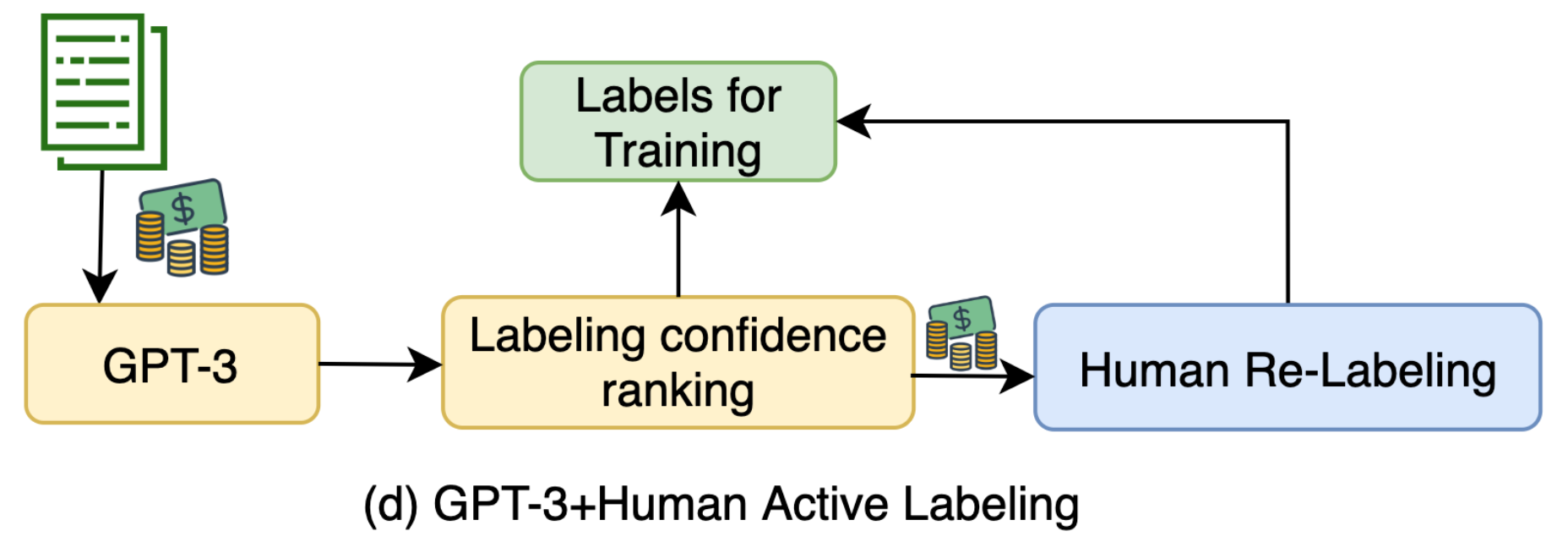
GPT-3所标记的不确定性较高的样本被发送给人工进行标记。小样本提示仅包含了少量的人工标记的样本，因此标记成本被限制了。合成样本通过预测的标签来进行排序，得分最低的样本被重新进行新一轮的标记流程。

GPT-3标签法在低成本区域取得了更好的结果，但是和预算充足的人工标记方法相比，性能还是有差距的。这就有了如下的不等式（虽然“很多”和“噪声”在不同任务上的含义是不一样的）：

许多高质量的数据 > 许多噪声数据 > 少量高质量数据

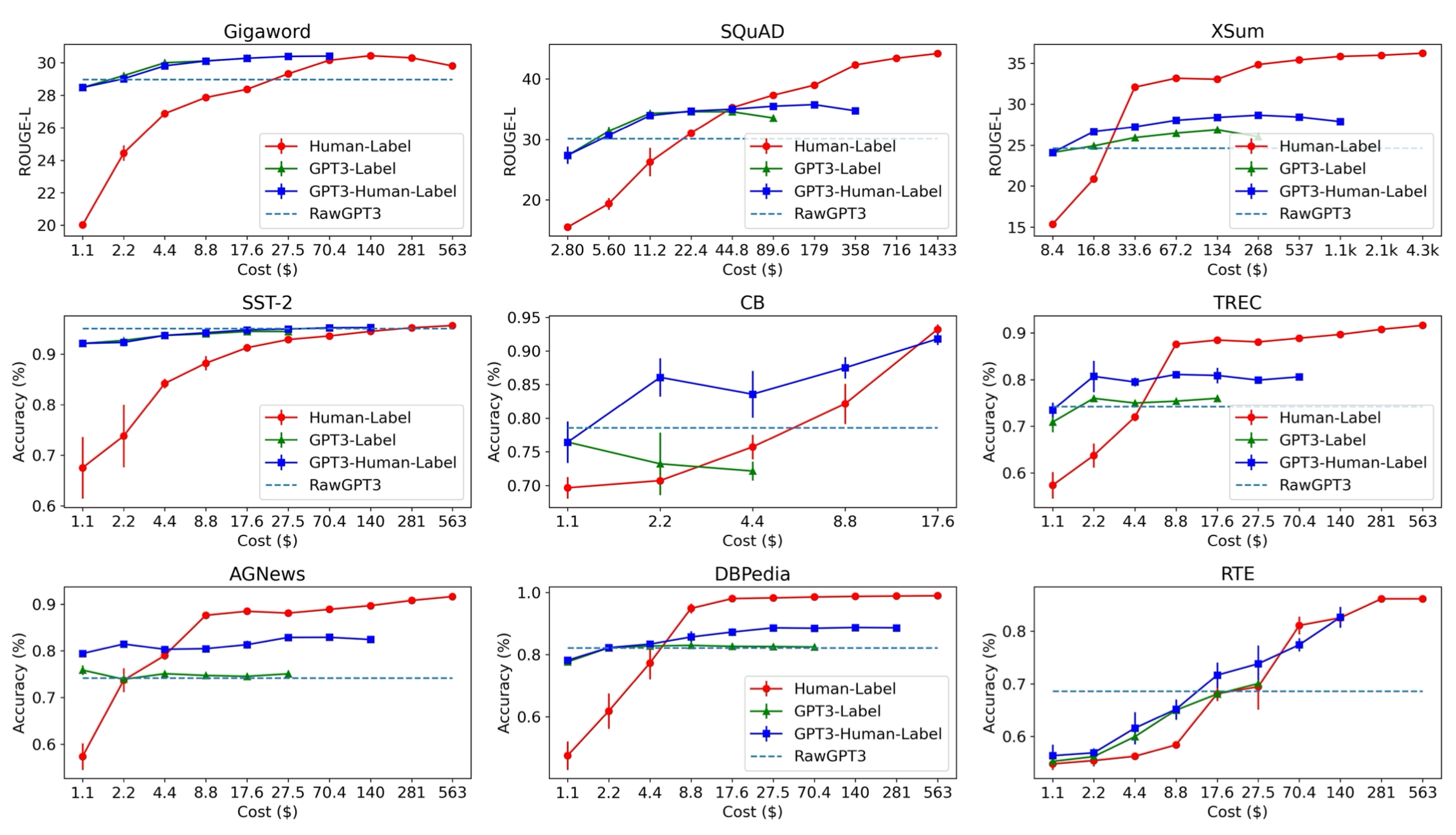
语言模型作为数据生成器

如果文本分类任务拥有足够的训练数据，我们可以对语言模型进行微调来基于标签来生成更多的训练数据（Anaby-Tavor 等, 2019,Kumar 等, 2021）。

基于语言模型的数据增强（Language-model-based data augmentation, LAMBADA;Anaby-Tavor 等, 2019）算法包含微调分类器和微调样本生成模型两个过程：

1. 使用现有训练数据集训练一个基线分类器：$h = \mathcal{A}(\mathcal{D}_\text{train})$
2. 独立于步骤1， 使用训练数据$\mathcal{D}_{train}$来微调语言模型$\mathcal{M}$，最终得到$\mathcal{M}_{\text{tuned}}$
3. 使用$\mathcal{M}_{tuned}$来对输入y[SEP]进行序列生成直到EOS，以此来合成一个标记数据集$\mathcal{D}^\star$
4. 过滤人工合成数据集
   1. 验证预测标签是否正确：$h(x) = y$
   2. 选择排位较高的样本（通过分类给出的概率）$\mathcal{D}_{syn} \subset \mathcal{D}^\star $。增强方法生成了10倍于所需的增强数据，仅保留置信度最高的前10%数据

最终的分类器在数据集$\mathcal{D}_\text{syn} \cup \mathcal{D}_\text{train}$上进行训练。此过程可以重复多次，但是收益是否会迅速消失或者是否会引入偏差并不是很清楚。

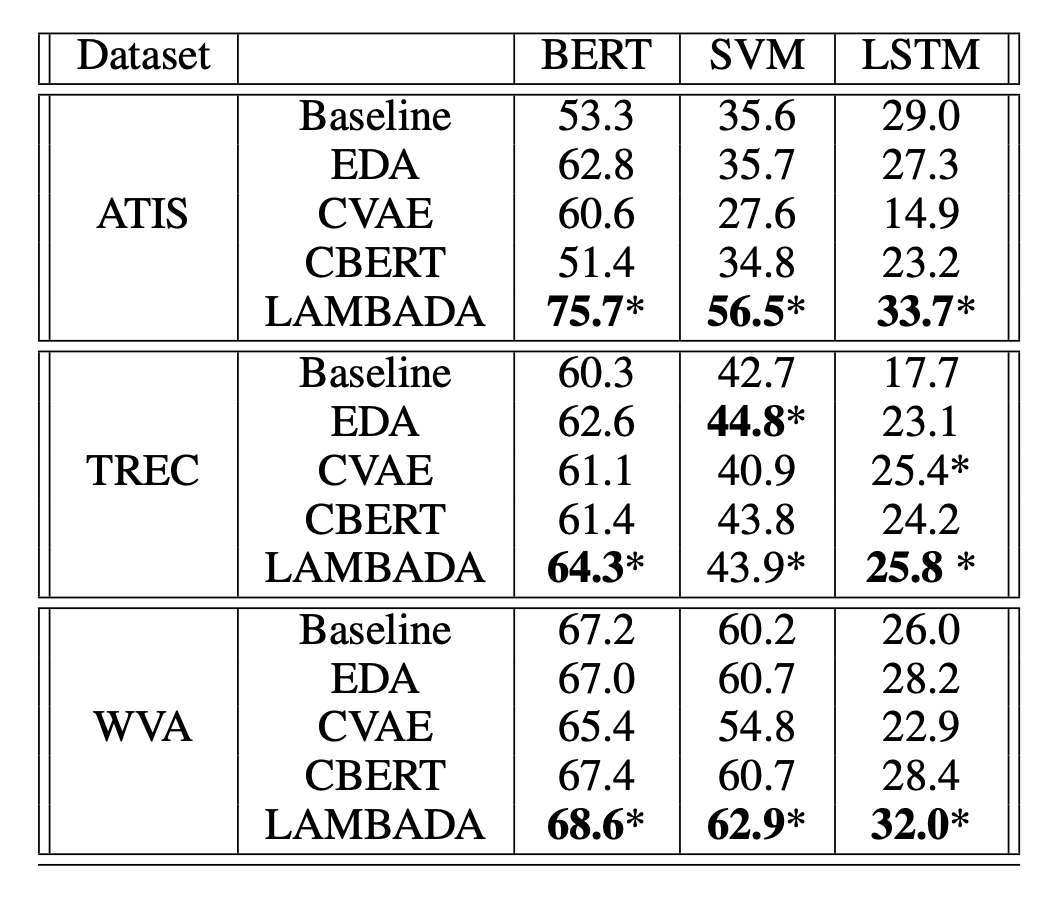
为了简化LAMBADA，我们可以消除待微调生成模型对现存的规模较大的训练数据集的依赖性（上面步骤2）。非监督数据生成（Unsupervised data generation, UDG;Wang 等, 2021）依赖于大预训练模型上的小样本提示（few-shot prompting）来生成高质量的合成数据。与上面的方法相反（LM使用$\mathbf{x}$作为输入来预测标签$y$），UDG使用标签$y$来合成数据$\mathbf{x}$。而后任务相关的模型就在此合成数据集上进行训练。

Schick & Schutze (2021)提出了一个相似的想法，但是应用在NLI任务上而非分类任务。它使用预训练语言模型来生成近似或者不同的句子对，同时模型使用特定任务的指令进行提示（prompted）。

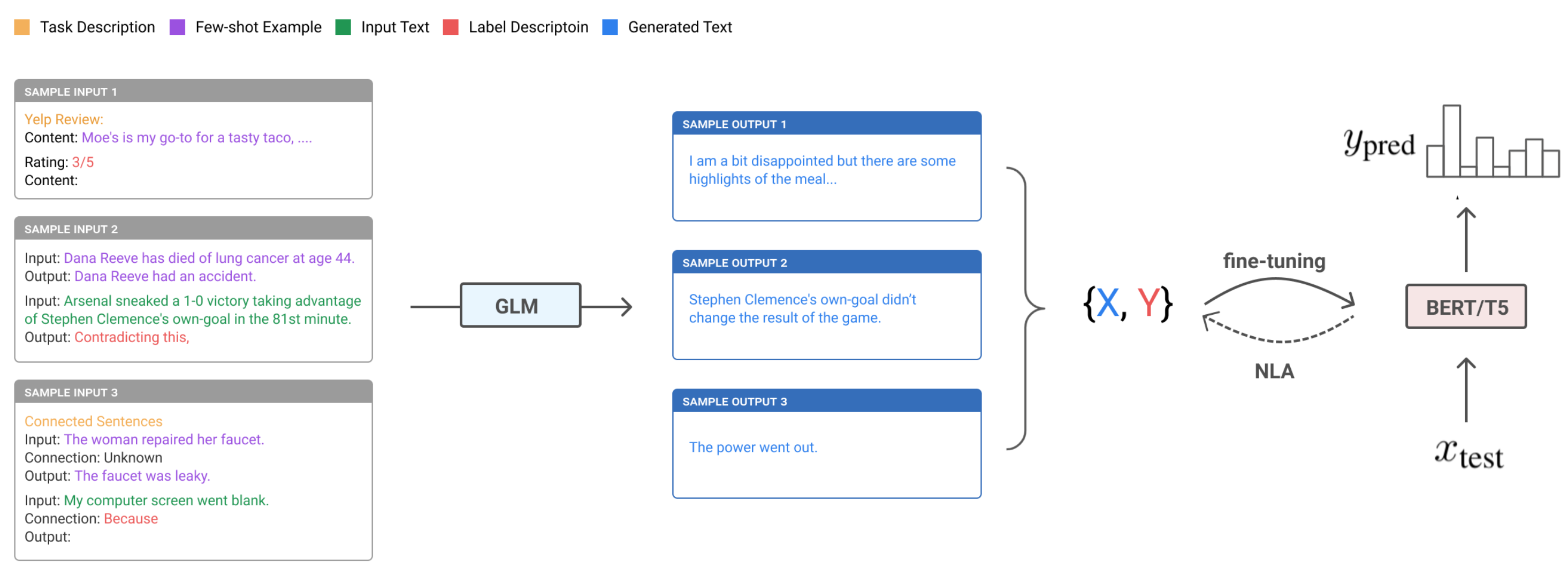
UDG的小样本提示包含少量的无标签样本以及特定任务相关标签的自然语言描述。由于一些生成的样本带有噪声，他们在训练过程中，使用噪声标签退火（Noisy Label Annealing, NLA）技术来过滤潜在的不对齐样本。NLA 在训练过程中，当模型开始以高置信度给出与伪标签不同的标签时，及时移除噪声（noisy）训练样本。在每一步$t$的训练中，一个样本$(\mathbf{x}_i, \hat{y}_i)$如果满足如下两个条件，那么它被认为是噪声（noisy）样本，需要被移除：

• 模型给出的的预测概率高于阈值：$p(\bar{y}_i \vert \mathbf{x}_i)\mu_t$, 其中$\bar{y}_i = \arg\max_y p(y \vert \mathbf{x}_i)$
• 生成的标签与模型给出的预测标签不等：$\bar{y}_i \neq \hat{y}_i$

注意，这里的阈值$\mu_t$是时间相关的，初始值设为0.9，并且随时间推移逐步退火至$\cfrac{1}{类别数量}$。

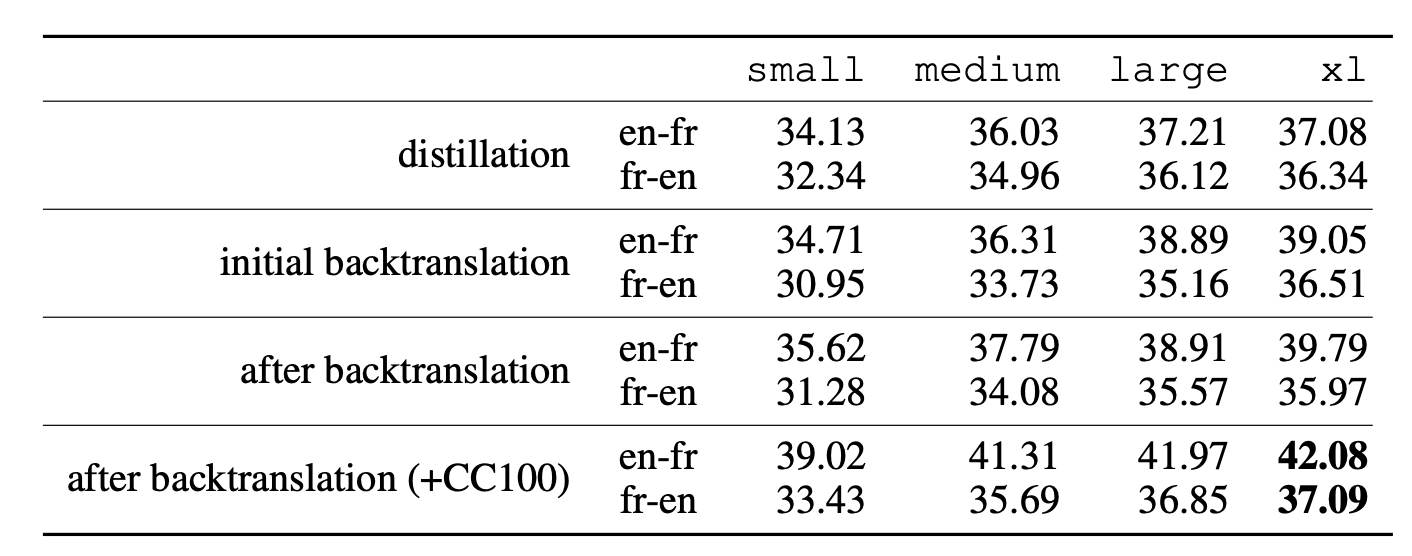
正如实验中展现的那样，UDG在小样本推断任务上带来的性能改善非常显著，此外NLA会带来一些额外的提升。方法最终的性能可以在一些情况下可以与监督学习的微调方法在同一水平线上。

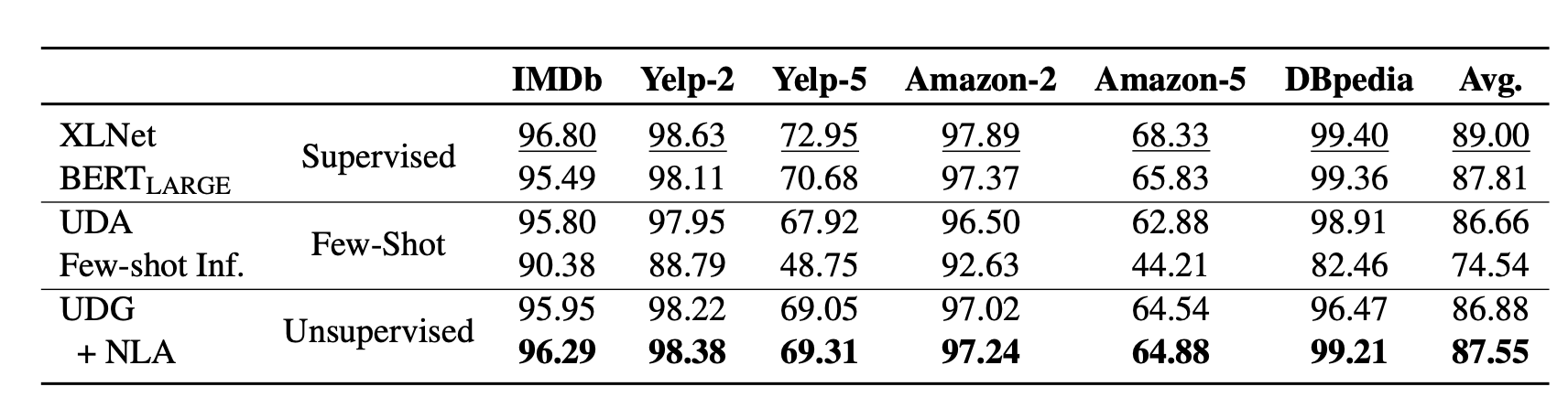
Han et al (2021)所提方法在翻译任务上获得了当前最好的表现，他们使用小样本数据生成、知识蒸馏以及回译的方法。他们的方法包含以下几个步骤（假定无法访问翻译的句子对）：

1. 零样本生成（zero-shot generation）：使用预训练语言模型的零样本翻译（zero-shot translation）能力来生成少量无标签句子的翻译
2. 小样本生成（few-shot generation）：拓展零样本翻译的结果，将它们用作小样本生成的输入以得到更多的人工合成数据
3. 蒸馏（distillation）：在所得数据集上微调模型。在给定一对不同语言的句子<seq1, seq2>，翻译任务被建模为一个语言模型任务：[L1] <seq1> [[TRANSLATE]] [L2] <seq2>.。在测试时，语言模型使用[L1] <seq> [[TRANSLATE]] [L2]作为提示（prompt），并且从完整的生成样本中得到一个候选翻译<sampledSeq>
4. 回译（back-translation）：继续在回译数据集上进行微调，此数据集中样本对的顺序被倒转：<sampledSeq, seq>
5. 重复上述1~4

上述方法的成功依赖于一个好的预训练模型来启动初始训练数据。小样本数据生成、蒸馏、回译的迭代过程是从预训练模型中提取翻译能力并将其蒸馏到一个新模型中的有效方式。

如何衡量生成数据的质量

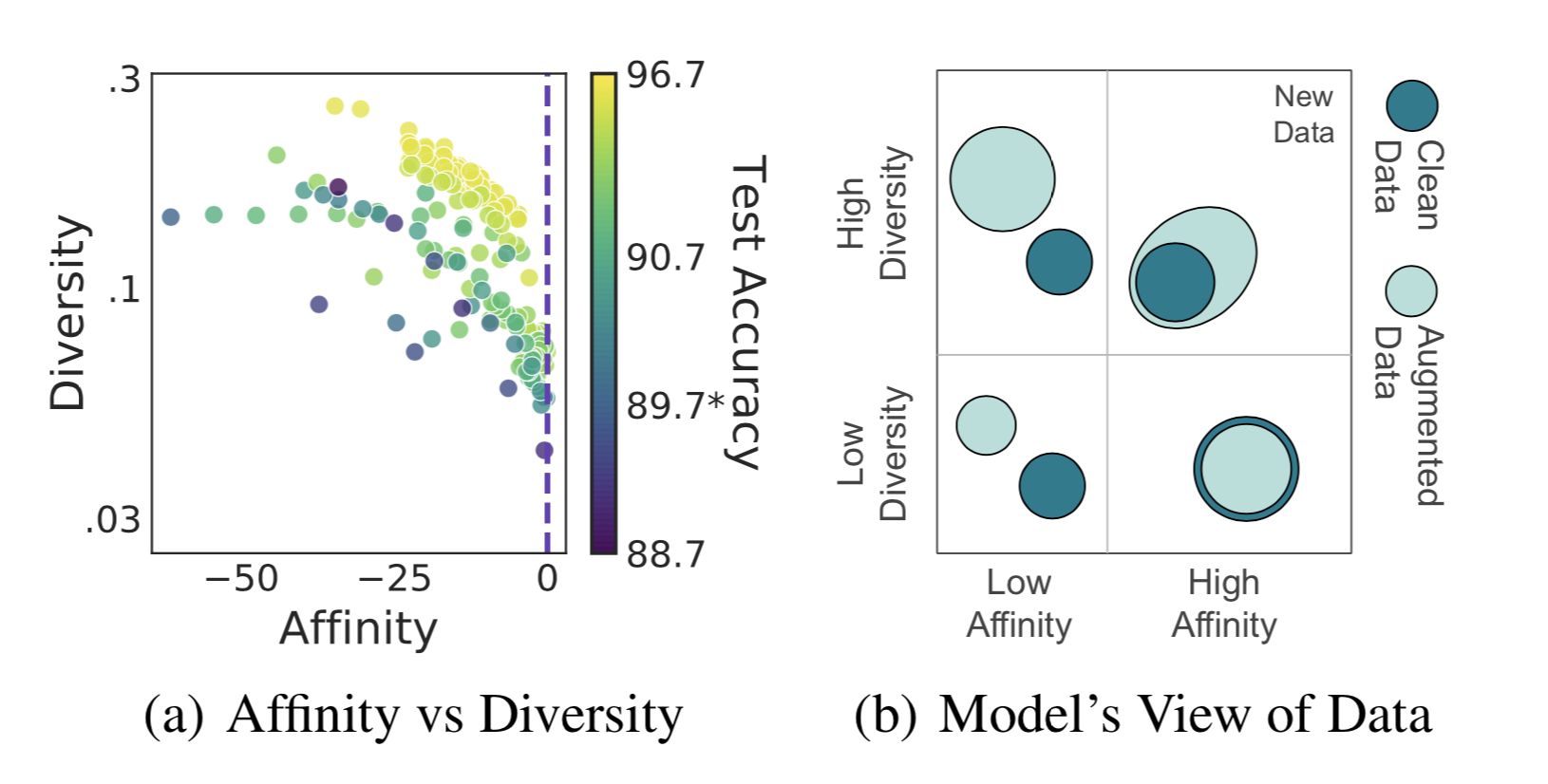
给定使用数据增强或者数据合成方法生成的数据，我们如何从改善模型范化性的角度来衡量数据质量呢？Gontijo-Lopes 等,2020从两个维度来考虑此问题，亲和度和发散度：

• 亲和度是用于衡量模型对分布偏移敏感性的指标，它可以量化增强操作在所生成的增强数据中引入的分布偏移的程度
  • 定义：模型在清洁数据（clean data）与增强数据间的性能差异（模型在清洁数据上进行训练）
  • 作为比较，KL散度也可以用于测量分布偏移，但是KL散度没有考虑到模型的性能
• 发散度是衡量增强复杂度的方法，它反映了增强数据相对于模型和学习进程的复杂度：
  • 定义：使用某个增强方法训练得到的模型的最终训练损失值
  • 其它可能的度量
    • 变换后数据的熵
    • 达到某个训练准确率阈值所需的模型训练时间
  • 上面提到的三个指标是相关的

最终模型的性能取决于这两个指标是否足够高。

现存有很多衡量相关度与发散度的指标，根据是否存在一个参考，它们有不同的形式，比如用于文本的 Perplexity/BLEU，用于图片的 inception 得分。这里跳过了一系列具体的衡量质量的指标，因为这会让文章非常长。

使用噪声数据进行训练

通过模型生成或数据增强，我们很容易生成大量的噪声数据。但是，我们很难保证这些数据是100%准确的。我们已知深度神经网络很容易过拟合噪声数据，并且“记住”错误的标签，我们可以在训练这些生成数据时应用训练噪声标签的技术（噪声鲁棒的训练）来稳定和优化性能。感兴趣的可以查看这篇关于从噪声标签中学习的综述（Song 等, 2021）来获取更多信息。

正则化以及鲁棒架构

简单讲，为了避免过拟合而设计的机制应该能够在训练轻度噪声数据时，帮助改善训练的鲁棒性，比如：权重衰减(weight decay)、批归一化(batch normalization)等。实际上，好的数据增强算法（也就是：仅有非核心属性被修改了）可以被看作是一种正则化的方式。

另一种方法是使用专用的噪声适配层来近似未知的标签损坏（label corruption） (Sukhbaatar 等, 2015,Goldberger & Ben-Reuven, 2017)。

Sukhbaatar 等, 2015在网络结构中引入了一个额外的线性层$Q$来适配模型的估计以匹配噪声标签的分布。噪声矩阵$Q$初始化为单位阵，并且训练开始阶段固定不变。一段时间后，$Q$被放开用于训练。经过正则化训练后，它可以匹配噪声的分布，并且同时保持基础模型对真实标签的预测准确率。

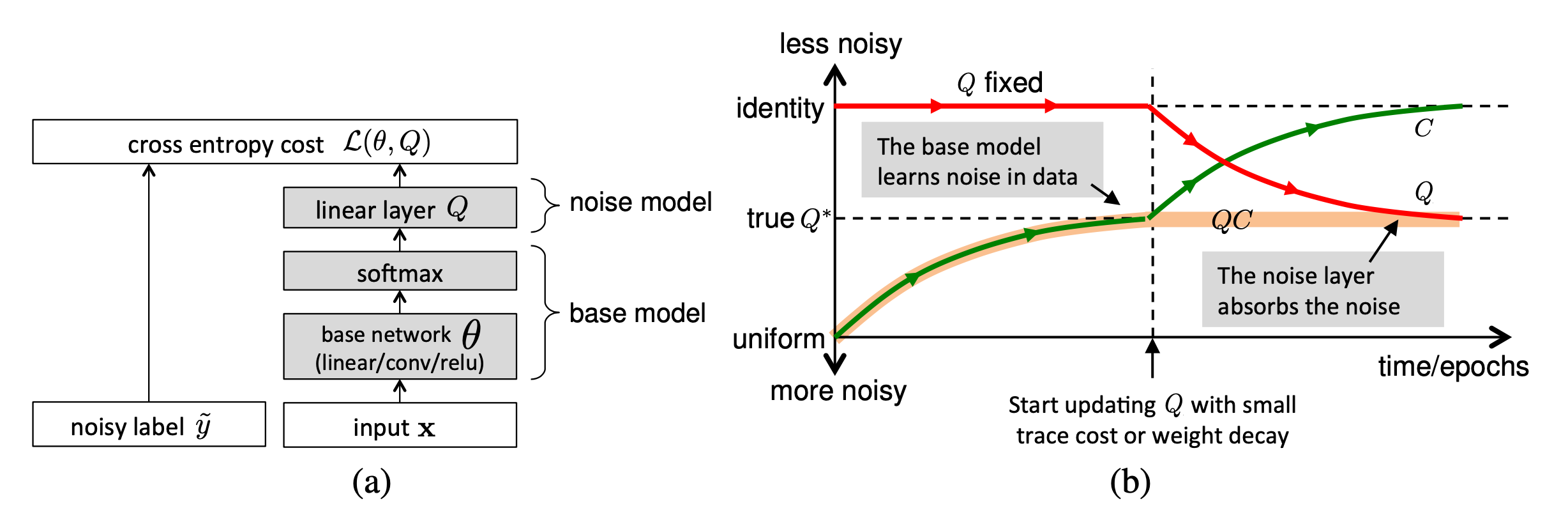
这里的一个问题是，无法保证此噪声矩阵仅捕获噪声带来的分布偏移，此外该矩阵其实很难学习。Goldberger & Ben-Reuven, 2017提出在基础模型上添加一个额外的端到端的softmax层，并且应用EM 算法。在使用EM算法时，他们将正确的标签视作隐随机变量，将噪声过程当作一个与未知参数通信的信道。

鲁棒的学习目标

除了最常用的交叉熵损失之外，其它一些学习目标可以更好地应对噪声标签。

举例来说，MAE（Mean Absolute Error）相比于CCE（Categorical Cross Entropy）在面对噪声标签时就更鲁棒，这是因为它平等地对待每一个样本（Ghosh 等,2017）。由于MAE在面对不同样本的时候缺乏权重分配机制，使用MAE进行模型训练所消耗的时间会极大地增加。为了在MAE和CCE之间能取得一个平衡，Zhang & Sabuncu, 2018提出了一个新的损失函数GCE（Generalized Cross Entropy），GCE相比于CCE来说可以更好地应对噪声数据。

为了同时得到MAE的噪声鲁棒性与CCE中内含的权重机制，GCE使用负Box-Cox变换作为损失函数：

其中$f^{(j)}$表示$f(\cdot)$的第$j$个元素，$q\in (0, 1]$。$\mathcal{L}_q$在$q \to 0$时与CCE等价，在$q=1$时变成MAE。实验显示，存在一个阈值，当$q$超过此阈值时过拟合不再出现。此外，数据中包含的噪声越多，该阈值越大。

给定真实和预测的标签$y_i, \hat{y}_i\in\{0, 1\}$，令$u_i = y_i \cdot \hat{y}_i$，那么0-1损失$\mathcal{L}_{01}(\mathbf{u}) = \sum_{i=1}^n \mathbb{1}[u_i<0]$>是另外一个对噪声数据展现出鲁棒性的学习目标。使用0-1损失来最小化经验风险（empirical resk）显示出与最小化经验敌对(最差)风险（empirical adversarial [worst-case] risk）(Hu 等, 2018)同样的性能。由于WCR（worst-case risk）是清洁数据（clean data）分布的分类风险的上界，最小化WCR意味着降低真正的风险，这就让0-1损失格外鲁棒。然而，0-1损失是不可导的，它不能直接进行优化。一个解决方案是近似出一个0-1损失的上界（可导），然后去最小化此上界。

Hinge 损失$\mathcal{L}_\text{hinge}(\mathbf{u}) = \sum_{i=1}^n \max(0, 1 - u_i)$定义了0-1损失的一个大致的上界。Lyu & Tsang, 2020提出了curriculum loss（CL），这是一个相比于传统的替代损失函数（比如hinge损失）更加紧致的上界：

其中，$\ell(u_i)$是0-1损失的一个基础替代损失（比如：hinge 损失），最优权重变量$\mathbf{w}$通过学习得到。

给定一个标签出错率（corruption rate）$\rho$，NPCL（noise pruned curriculum loss）基于如下观察构建：理想的模型应该正确分类$n(1-\rho)$个正确标签的样本，但是错误分类$n\rho$个错误标签的样本。如果$\rho$是一个已知的先验值，我们会知道有多少样本（loss值最大）应该被裁剪掉。假设$\ell(u_1) \leq \dots \leq \ell(u_n)$，有$u_{n(1-\rho)+1} = \dots = u_n =0$，那么下面的NPCL仅是$n(1-\rho)$个样本的基础CL：

在CIFAR-10的实验上，NPCL和GCE取得了不相上下的结果，并且在噪声率增加时甚至表现更佳。

标签修正

由于已知一些标签是错误的，噪声鲁棒的训练可以显式地将标签修正纳入考虑之内。

一个方法是依赖于一个噪声转移矩阵的估计来修正前向或后向损失，称作F-correction（Patrini 等, 2017）。首先，我们假定：存在$k$个类别；噪声转移矩阵$C \in [0, 1]^{k\times k}$是可观测的；标签翻转概率不依赖于样本输入而仅依赖标签（通常被称作RCN, random classification noise）。令$\tilde{y}$表示一个出错的标签，$C$的每个值表示标签翻转为另外一个标签的概率：

然后，我们在预测时使用此噪声转移矩阵的先验知识，进行一个前向标签修正过程。

用矩阵符号，我们有$\mathcal{L}(\hat{p}(y \vert \mathbf{x})) = - \log C^\top \hat{p}(y \vert \mathbf{x})$。然而，这样一个噪声转移矩阵通常是未知的。如果我们可以得到一个干净的数据集，那么噪声矩阵$C$可以通过在清洁数据上计算混淆矩阵来得到一个估计（Hendrycks 等, 2018）。我们使用$\mathcal{D}_c$表示一个可信的清洁数据集，使用$\mathcal{D}_n$表示噪声数据集。

其中$\mathcal{A}_i$是$\mathcal{D}_c$中标签为$i$的数据点的子集。

令$f(x) = \hat{p}(\tilde{y} \vert \mathbf{x}; \theta)$，那么模型可以在清洁数据集$\mathcal{D}_c$上使用损失函数$\mathcal{L}(f(\mathbf{x}), y)$，在噪声数据$\mathcal{D}_c$上使用损失函数$\mathcal{L}(\hat{C}^\top f(\mathbf{x}), \hat{y})$。

如果可信的训练集$\mathcal{D}_c$非常大，那么我们可以仅用清洁数据训练一个神经网络，而后将此神经网络的知识通过正确的伪标签（Li 等, 2017），蒸馏到一个主模型（primary model）中（也就是用于最终测试的模型）。主模型是使用整个数据集$\mathcal{D} = \mathcal{D}_c \cup \mathcal{D}_n$进行训练得到的。此外，我们还可以用一些从知识图谱中获取的标签关系信息来辅助知识蒸馏过程，以让在有限数据上训练的网络的预测更加鲁棒。

标签修正蒸馏过程工作方式如下：

1. 首先使用一个小的清洁数据集$\mathcal{D}_c$来训练一个辅助模型$f_c$，并使用此模型为所有样本$x_i$提供一个软标签，$s_i = \delta(f_c(\mathbf{x}_i)/T)$为带温度值$T$的sigmoid激活函数
2. 由于$\mathcal{D}_c$数据集不大，$f_c$很有可能过拟合。Li等, 2017借助知识图谱$\mathcal{G}$来定义标签空间中的关系，并且在相应的标签中传播预测值。新的软标签为$\hat{s}_i = \mathcal{G}(s_i)$
3. 主模型$f$使用$f_c$的预测值进行模仿训练：

样本选择及权重修正

一些样本可能相比于其它样本更有可能有不准确的标签。这种预估可以帮助我们去判断哪些样本应该设置较多/较少的权重。考虑训练数据中的两类偏差：类别不平衡与噪声标签，那么实际上存在着一个相互冲突的偏好：我们更加喜欢损失值较大的样本来平衡标签分布，但是那些损失值较小的样本却可以缓解潜在的噪声。因此，一些工作（Ren 等, 2018）认为为了学习到训练数据偏差的一般式，有必要使用一个小的无偏验证来指导训练。本小节介绍的样本重新加权的方法都假设可以访问到一个小的、可信的干净数据集。

考虑一个带随机噪声的二进制分类任务，$y, \hat{y} \in \{-1, +1\}$，标签翻转概率为：$\rho_{-1}, \rho_{+1} \in [0, 0.5)$定义为：

Liu & Tao, 2015应用重要性重加权（importance reweighting）来调整观察到的$\hat{y}$的权重分布来匹配不可观察的$y$的分布。令$\mathcal{D}$为真实数据分布，$\mathcal{D}_\rho$为带错误版。

因为：

因此赋予噪声样本的权重为：

其中$P_{\mathcal{D}_\rho}(\tilde{y} \vert \mathbf{x})$可以使用简单的逻辑回归来估计，但是估计噪声占比更具挑战性。朴素的交叉验证可以工作，但是它的代价比较大，因为它依赖于可信标签数据的数量。这篇论文首先近似了噪声比例的一个上界$\rho_\tilde{y} \leq P_{\mathcal{D}_\rho}(- \tilde{y} \vert \mathbf{x})$，而后使用一个假设来有效地估计它：$\hat{\rho}_{\tilde{y}} = \min_{\mathbf{x} \in {\mathbf{x}_1, \dots, \mathbf{x}_n}} \hat{P}_{\mathcal{D}_\rho}(- \tilde{y} \vert \mathbf{x})$。在他们的实验中，重要性重加权的优势仅因数据集而异，并且一般情况下此法在噪声占比较高时更加有效。

样本重加权方案可以通过一个单独的网络来学习得到。学习重加权（Learning to Reweight,L2R;Ren 等, 2018）是一个元学习（meta-learning）方法，它通过在已知干净数据集上的性能表现来直接优化权重。每个样本基于其梯度的方向得到一个权重值。待训练的权重集参数为$\{w_i\}_{i=1}^n$，权重损失函数$\theta^*(\mathbf{w})$的训练目标为最小化在无偏的验证集$\mathcal{D}_c = \{x^\text{valid}_j\}_{j=1}^m$上的损失：

学习过程包含了两个嵌套的优化循环，因此代价较大，大概需要三倍的训练时间。

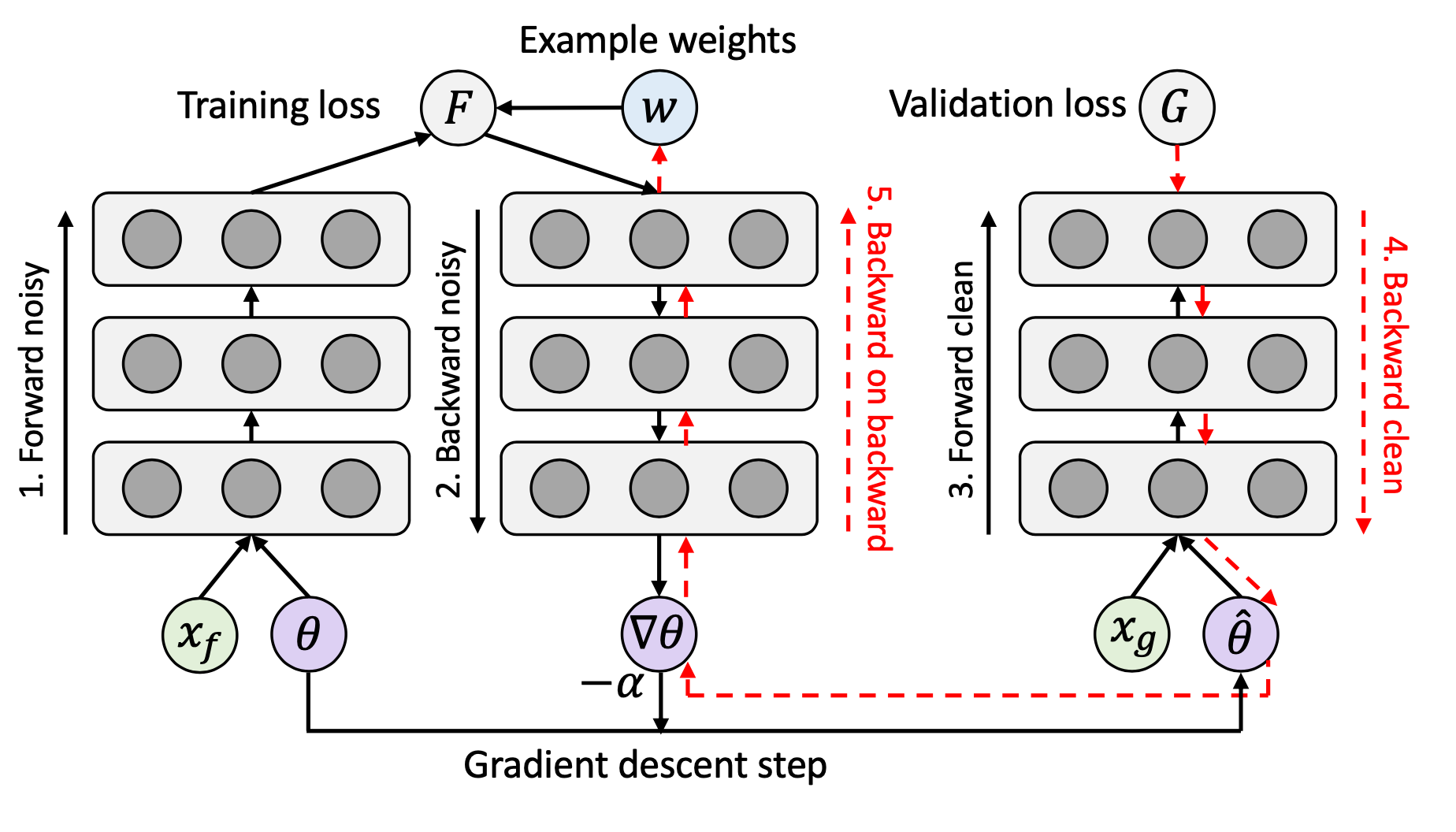
他们在两个数据集上进行了训练：

1. 使用分布不均的二分类MNIST数据集来测试L2R的鲁棒性
2. 带噪声标签的CIFAR-10数据集

L2R在这两个任务上都超过了基线方法。

MentorNet（Jiang 等, 2018）使用导师-学生模型来进行数据加权。他们运用了两个不同的网络：一个导师一个学生。导师网络为学生网络提供了一个数据驱动的指导（也就是样本加权方案），让学生聚焦在如何学习正确的标签上。

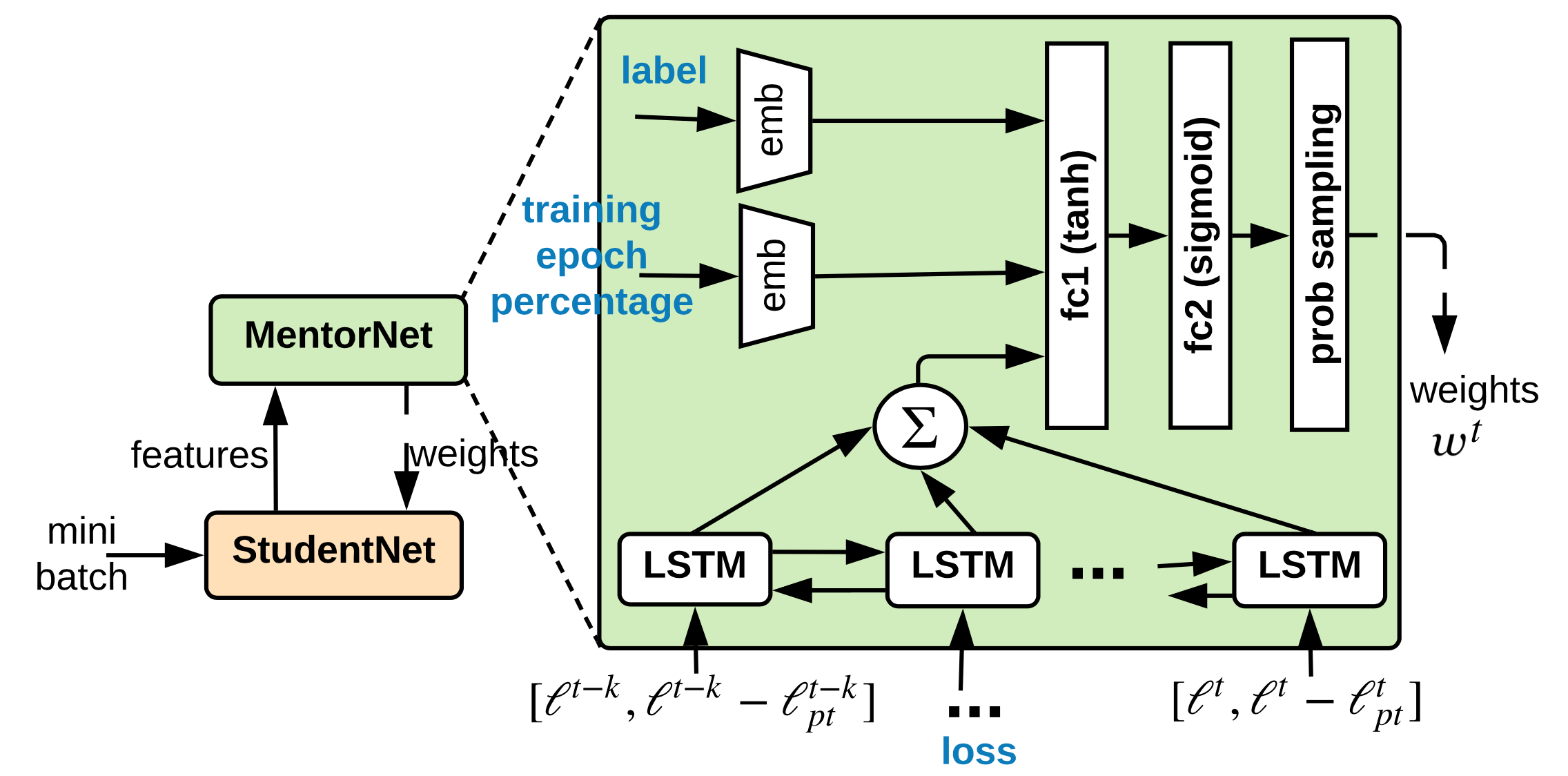
令$g_\psi$为参数为$\psi$的MentorNet，$f_\theta$为参数为$\theta$的StudentNet，$G$为一个参数为$\lambda$的预定义的“指导课程”。给定一个$k$分类任务的训练集$\mathcal{D} = \{(\mathbf{x}_i, y_i)\}_{i=1}^n$，MentorNet的输入为StudentNet$f$处理得到的一个中间特征$\mathbf{z}_i = \phi_{f_\theta}(\mathbf{x}_i, y_i)$，并用其预测一个随时间变化的隐权重变量$\mathbf{w} \in [0, 1]^{n \times k}$来指导StudentNet的学习：

StudentNet 最小化如下损失函数：

导师网络$g_\psi$使用交叉熵损失来训练，输入为$(\phi_{f_\theta}(\mathbf{x}_i, y_i), w^{*}_i)$，其中如果已知$y_i$为正确的标签，那么$w_i^\star = 1$，否则设置为$0$。MentorNet的网络结构不必非常复杂。在论文中，他们使用了一个LSTM层来捕获随时间变化的预测值。

在MentorNet方法中，一个网络会去为另一个网络显式地去学习加权方案。Co-teaching（Han 等, 2018）方法同时训练了两个神经网络$f_1, f_2$，并且它们之间互相喂经过挑选的数据。Co-teaching 由以下三步组成：

1. 首先，每个网络对mini-batch 数据进行前向求值，并且选择潜在可能的带正确标签的数据
2. 两个网络交换挑选的数据信息。损失值较小的样本被挑选出来，因为他们更可能是正确的。被选择样本的百分比由一个时间函数$R(T)$决定。由于随着不断地训练，网络更加容易过拟合并且更容易记住噪声标签，因此，$R(T)$的值会随着时间推移而逐渐变小。通过这样的方式，我们可以保证选择出高质量的数据。

根据他们的实验结果，在噪声比例较高或者错误转移矩阵为非对称时，co-teaching的性能超过了F-correction。

引用格式：

@article{weng2022datagen,
  title   = "Learning with not Enough Data Part 3: Data Generation",
  author  = "Weng, Lilian",
  journal = "lilianweng.github.io",
  year    = "2022",
  url     = "https://lilianweng.github.io/posts/2022-04-15-data-gen/"
}

参考文献

[1] Zhang et al.“Adversarial AutoAgument”ICLR 2020.

[2] Kumar et al.“Data Augmentation using Pre-trained Transformer Models."AACL 2020 Workshop.

[3] Anaby-Tavor et al.“Not enough data? Deep learning to rescue !"AAAI 2020.

[4] Wang et al.“Want To Reduce Labeling Cost? GPT-3 Can Help."EMNLP 2021.

[5] Wang et al.“Towards Zero-Label Language Learning."arXiv preprint arXiv:2109.09193 (2021).

[6] Schick & Schutze.Generating Datasets with Pretrained Language Models."EMNLP 2021.

[7] Han et al.“Unsupervised Neural Machine Translation with Generative Language Models Only."arXiv preprint arXiv:2110.05448 (2021).

[8] Guo et al.“Augmenting data with mixup for sentence classification: An empirical study."arXiv preprint arXiv:1905.08941 (2019).

[9] Ekin D. Cubuk et al.“AutoAugment: Learning augmentation policies from data."arXiv preprint arXiv:1805.09501 (2018).

[10] Daniel Ho et al.“Population Based Augmentation: Efficient Learning of Augmentation Policy Schedules."ICML 2019.

[11] Cubuk & Zoph et al.“RandAugment: Practical automated data augmentation with a reduced search space."arXiv preprint arXiv:1909.13719 (2019).

[12] Zhang et al.“mixup: Beyond Empirical Risk Minimization."ICLR 2017.

[13] Yun et al.“CutMix: Regularization Strategy to Train Strong Classifiers with Localizable Features."ICCV 2019.

[14] Kalantidis et al.“Mixing of Contrastive Hard Negatives”NeuriPS 2020.

[15] Wei & Zou.“EDA: Easy data augmentation techniques for boosting performance on text classification tasks."EMNLP-IJCNLP 2019.

[16] Kobayashi.“Contextual Augmentation: Data Augmentation by Words with Paradigmatic Relations."NAACL 2018

[17] Fang et al.“CERT: Contrastive self-supervised learning for language understanding."arXiv preprint arXiv:2005.12766 (2020).

[18] Gao et al.“SimCSE: Simple Contrastive Learning of Sentence Embeddings."arXiv preprint arXiv:2104.08821 (2020). [code]

[19] Shen et al.“A Simple but Tough-to-Beat Data Augmentation Approach for Natural Language Understanding and Generation."arXiv preprint arXiv:2009.13818 (2020) [code]

[20] Wang & van den Oord.“Multi-Format Contrastive Learning of Audio Representations."NeuriPS Workshop 2020.

[21] Wu et al.“Conditional BERT Contextual Augmentation”arXiv preprint arXiv:1812.06705 (2018).

[22 Zhu et al.“FreeLB: Enhanced Adversarial Training for Natural Language Understanding."ICLR 2020.

[23] Affinity and Diversity: Quantifying Mechanisms of Data Augmentation Gontijo-Lopes et al. 2020 (https://arxiv.org/abs/2002.08973)

[24] Song et al.“Learning from Noisy Labels with Deep Neural Networks: A Survey."TNNLS 2020.

[25] Zhang & Sabuncu.“Generalized cross entropy loss for training deep neural networks with noisy labels."NeuriPS 2018.

[26] Goldberger & Ben-Reuven.“Training deep neural-networks using a noise adaptation layer."ICLR 2017.

[27] Sukhbaatar et al.“Training convolutional networks with noisy labels."ICLR Workshop 2015.

[28] Patrini et al.“Making Deep Neural Networks Robust to Label Noise: a Loss Correction Approach”CVPR 2017.

[29] Hendrycks et al.“Using trusted data to train deep networks on labels corrupted by severe noise."NeuriPS 2018.

[30] Zhang & Sabuncu.“Generalized cross entropy loss for training deep neural networks with noisy labels."NeuriPS 2018.

[31] Lyu & Tsang.“Curriculum loss: Robust learning and generalization against label corruption."ICLR 2020.

[32] Han et al.“Co-teaching: Robust training of deep neural networks with extremely noisy labels."NeuriPS 2018. (code)

[33] Ren et al.“Learning to reweight examples for robust deep learning."ICML 2018.

[34] Jiang et al.“MentorNet: Learning data-driven curriculum for very deep neural networks on corrupted labels."ICML 2018.

[35] Li et al.“Learning from noisy labels with distillation."ICCV 2017.

[36] Liu & Tao.“Classification with noisy labels by importance reweighting."TPAMI 2015.

[37] Ghosh, et al.“Robust loss functions under label noise for deep neural networks."AAAI 2017.

[38] Hu et al.“Does Distributionally Robust Supervised Learning Give Robust Classifiers? “ICML 2018.