

当前,深度神经网络模型越来越大,这导致了训练时会消耗更多的内存、显存。在使用显卡进行计算加速时,显存的大小极大地限制了深度学习模型的大小。当前,常见的NVIDIA显卡显存为4GB / 6GB / 8GB / 12GB / 24GB等,这些显存远不能满足当前很多深度学习模型。目前已有一些解决此问题的方法,本文所提方法的主要思想是使用少量的CPU计算换取内存(显存)的节省。
文章目录
- 简介
- 基于计算图的内存优化
- 计算图
- 替换与共享
- 计算换存储
- 丢弃计算量小的中间结果
- 复杂度分析
- 递归优化
- 深度学习框架建议
- 实验结果
- 引用
简介
在神经网络的训练过程中,通常神经网络本身参数所消耗的内存要远小于所保存的中间结果消耗的内存。因此,本文的重点也是放在如何减少中间变量存储上的。本文通过对神经网络对应的计算图的分析,来降低内存的消耗。文中提出的方法可以通过引入少量额外的计算来大幅降低内存的消耗。对于一个n层的神经网络来说,理论上可以用使用额外的一轮前向网络计算来获得仅需$O(\sqrt n)$的内存消耗,相比于无优化条件下$O(n)$的消耗,内存使用量大大减少。
降低内存消耗,不仅可以训练更大的模型,而且还可以让用户使用更大的 batch size,这可以增加模型训练过程的稳定性。对于原本一些需要进行模型并行但不太大的模型来说,使用本文的方法后,可以使用更加简单高效的数据并行进行训练。
对于如何训练大模型,还有其它很多方法,比如使用内存/显存交换、模型并行等。这些方法和本文提出的方法不冲突,可以同时使用,以带来最优的优化效果。而且本文提出的方法无需占用额外的PCI-E通信带宽,这就可以将这些带宽让给模型、数据并行来使用。
基于计算图的内存优化
计算图
神经网络可以用一张计算图来表示。在计算图中,节点表示一个计算操作,边表示一个依赖关系。下图展示了一个两层的神经网络的简化的计算图:
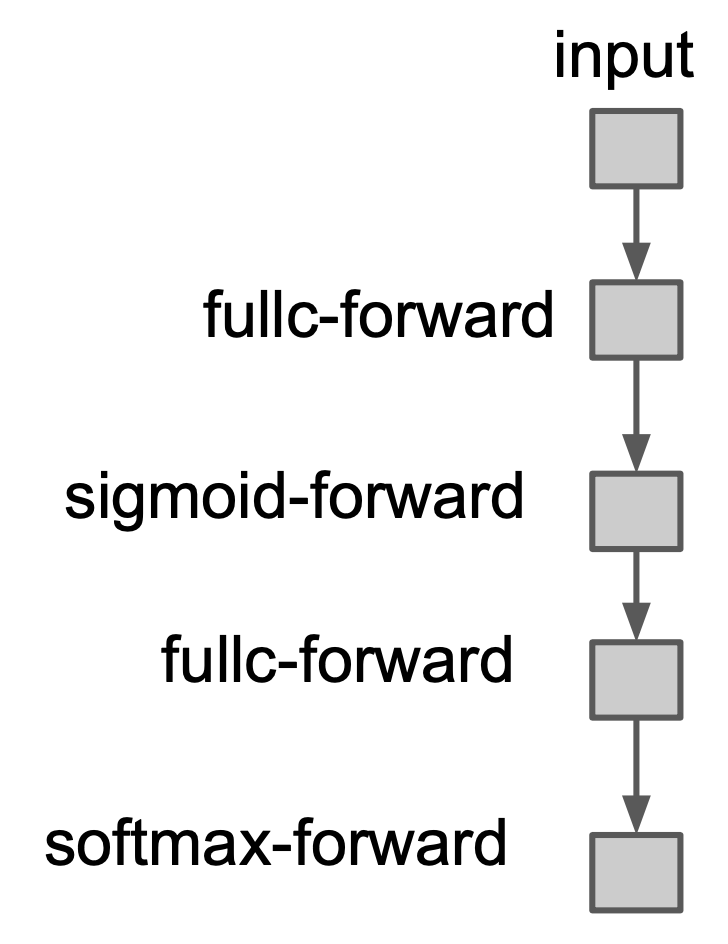
上图仅包含了前向的计算操作,可以看到每一步操作都依赖于前一步操作。引入反向传播的计算后,计算图表示如下:

可以看到,在带有反向传播的计算图中,一个明显的不同就是,一个计算节点会存在多个依赖,这对于下面我们介绍的内存优化很重要。
替换与共享
一般情况下,我们训练神经网络的时候,大部分消耗的内存会被用于存储计算的中间变量,比如前向计算的时候,我们需要存储每一步的中间结果,这些中间结果可能会在后续被用到。每个中间计算结果都对应了计算图中的某个节点。好的内存分配算法应该可以充分利用内存空间,对于一些后续不再用到的数据空间,应该释放或者重用。通常情况下有两种内存优化的方法:
- 替换操作:直接将现有输出的中间值保存到已经被分配的内存中去
- 内存共享:在中间结果之间进行内存的共享,也就是说将后续的中间结果保存在已经分配的但后续不会再用到的之前的内存中
下面我们首先看与上图对应的一个内存分配的一个例子:
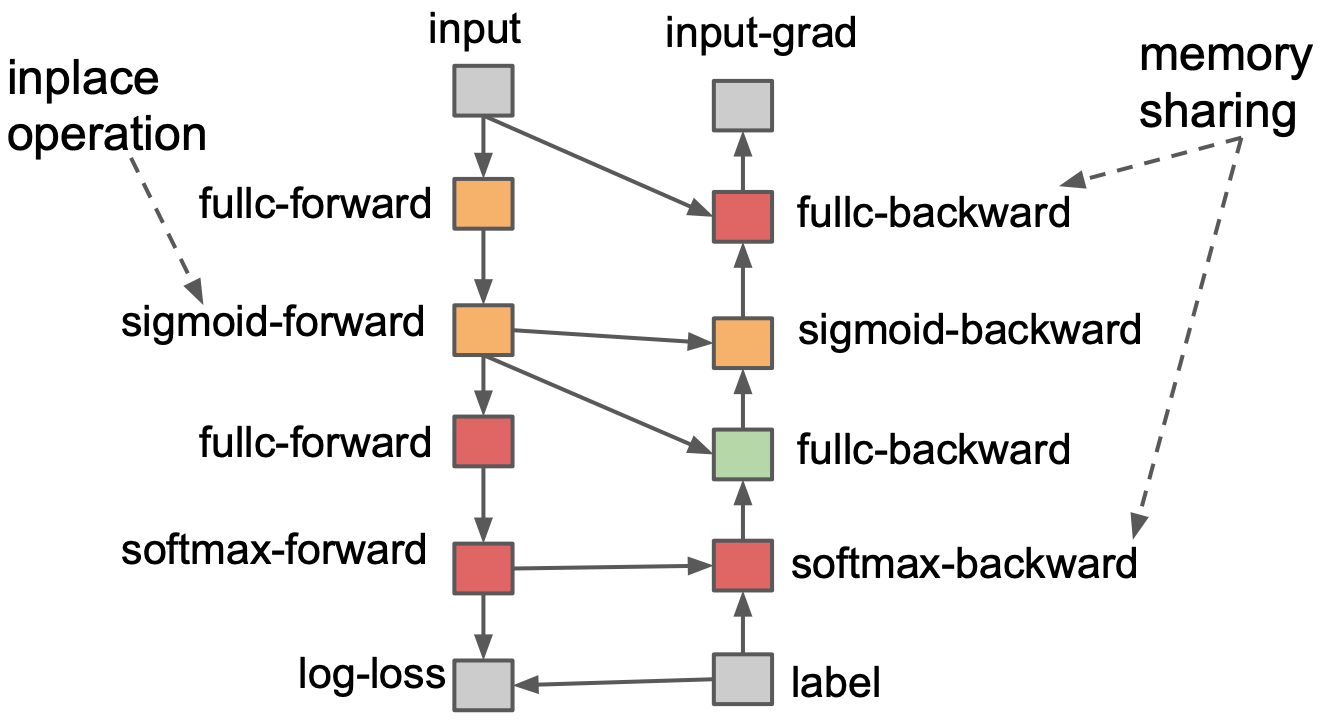
图中同样的彩色颜色表示共享了内存。对于替换和共享两种方案,图中都有表示。
对于替换操作:图中fullc-forward操作的结果和sigmoid-forward的操作结果中的值都是一一对应的,占用同等大小的内存,并且fullc-forward操作仅会被sigmoid-forward操作依赖,后续没有计算再会用到fullc-forward操作的结果。因此,此时可以直接将sigmoid-forward计算的结果保存到之前分配给fullc-forward的内存中去。
对于共享操作:我们看右半边的backward部分,可以看到在进行最上层的fullc-backward操作时,下面的softmax-backward的输出结果已经不会被再用到了,此时就可以重用该部分内存用于保存fullc-backward的结果。
文中提出的算法使用拓扑排序算法遍历计算图,并且对于每个操作节点进行引用计数,以便确定该节点的存储是否可以被释放重用。在实际使用时,可以预先计算所有操作会消耗的内存大小,这样就可以避免内存回收过程而直接共享内存空间。 因此,对于深度学习框架来说,需要做好两件事:
- 构建一个最小依赖的计算图
- 在计算过程中分析依赖图中,中间结果是否还存在后续依赖以决定内存是否可以被共享
计算换存储
上面提到的方法,虽然可以降低一定的内存消耗,但是从算法复杂度来讲,对于一个n层的神经网络来说,仍然需要消耗$O(n)$的内存空间。为了降低内存消耗的复杂度,本文提出了一种新的降低内存消耗的方法。该方法会丢弃部分中间计算结果,而这些中间结果在后续可以通过再次计算而获得,这样就可以通过计算来降低中间结果存储消耗的内存了。
具体来说,一个神经网络被分成了多个段,每一个段中包含了多个层。对于一个段来说,我们只保存该段的最终输出结果,而将段中的计算结果丢弃掉。这些中介结果在需要的时候可以使用该段的输入再进行额外的重新计算得到。具体算法如下python伪代码所示:
def backgrop_with_data_drop(inputx, segments, label):
v = inputx
# seg_inputs 用于存储每一个段的输入
seg_inputs = {}
for k in range(len(segments)):
seg_inputs[k] = v
for layer in segments.layers:
v = layer.forward(v)
grad = gradient(v, label)
for k in range(len(segments) - 1, -1, -1):
# 获取段k的输入
v = seg_inputs[k]
# 计算段k的中间结果
seg_middle_outs = {}
segment = segments[k]
for i in range(len(segment.layers) - 1):
seg_middle_outs[i] = v
v = segment.layers[i].forward(v)
# 利用计算好的中间结果,计算段k中所有层梯度
for i in range(len(segment.layers) - 1, -1, -1):
g = layer[i].backward(g, seg_middle_outs[i])
算法流程很明了,此处不再赘述。
该算法存在两个问题:
- 用户必须手动对计算图进行分割,以及编写循环代码
- 算法无法使用前面提到的替换操作和共享操作来进行内存优化
对此,本文提出了第二个改进算法。由于本人的学渣体质,对于论文中给出的算法并没有看懂,感兴趣的同学可以去看原论文。如果有同学看懂了,还请留言赐教。
在论文介绍改进算法的章节中,还提到了以下几个方面。
丢弃计算量小的中间结果
对于这一点很好理解,对于一些十分容易计算的操作来说,中间结果没有必要浪费内存来保存,比如pooling、激活函数操作、batch normalization等等。
复杂度分析
对于一个n层的神经网络,将其分为k段后,那么内存消耗为:
total-cost = max(cost-of-segment(i)) + O(k)
= O(n/k) + O(k)
= O(sqrt(n)) # 此处取 k = sqrt(n)
因此,使用该算法,内存复杂度可以优化到$O(\sqrt{n})$,而所需的代价就是额外增加一次前向计算来获取丢弃的中间结果。
递归优化
该方法指的是,我们对于一个计算图进行上述分段之后,那么我们把得到的每一段都看作一个计算操作的节点。这些新的段节点对于整个图来说是相对独立的存在,此时可以将段节点内的所有操作当作一个新的计算图来进行优化,这就是递归优化的基本思想。
深度学习框架的建议
- 添加选项供用户选择,以丢弃一些计算量极小的中间变量,来优化内存
- 提供内存(显存)规划算法,以提供高效的内存(显存)分配
- 第三点与改进算法本身有关,并且该项并不是必要的,感兴趣可以查看原论文
实验结果
文中对比了以下策略:
- 无优化 (no optimization)
- 当可能时,使用替换操作 (inplace)
- 使用替换操作 + 共享操作 (sharing)
- 上述优化 + 丢弃 batch norm和relu的结果 (drop bn, relu)
- 上述优化 + 本文提出的计算换存储的算法 (sublinear plan)
ResNet 结果
文中测试了ResNet在使用不同层数的残差层时的结果。
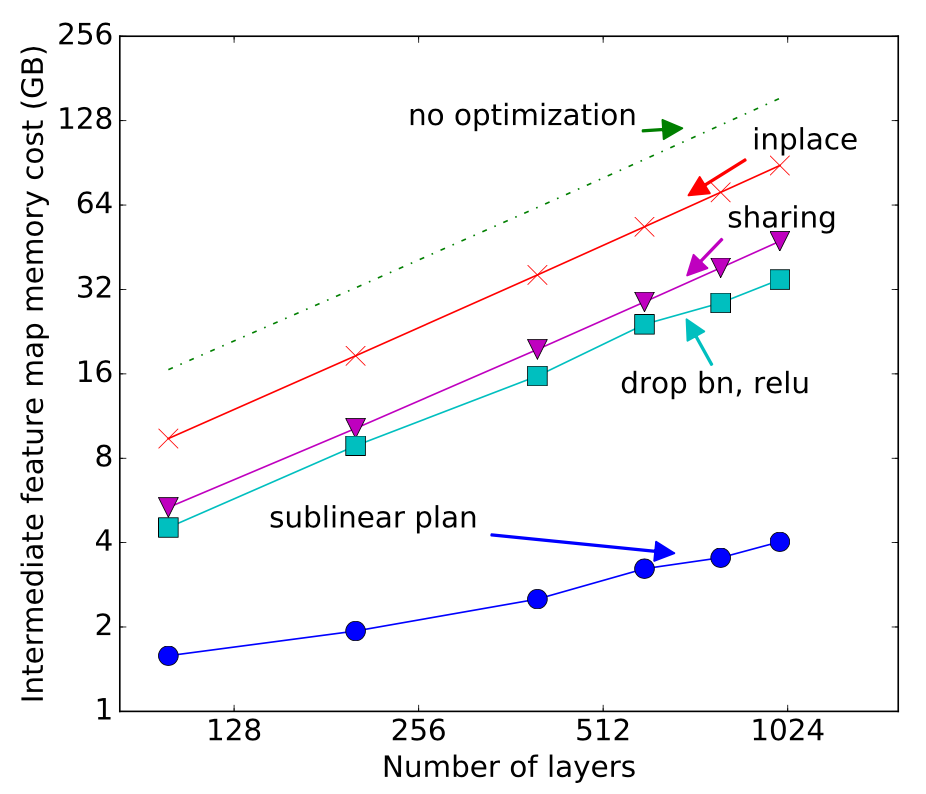
这里的内存消耗是根据静态内存分配方案得到的,可以看到本文提出的方案优势极为明显。
下图展示了实际运行时的显存消耗情况:
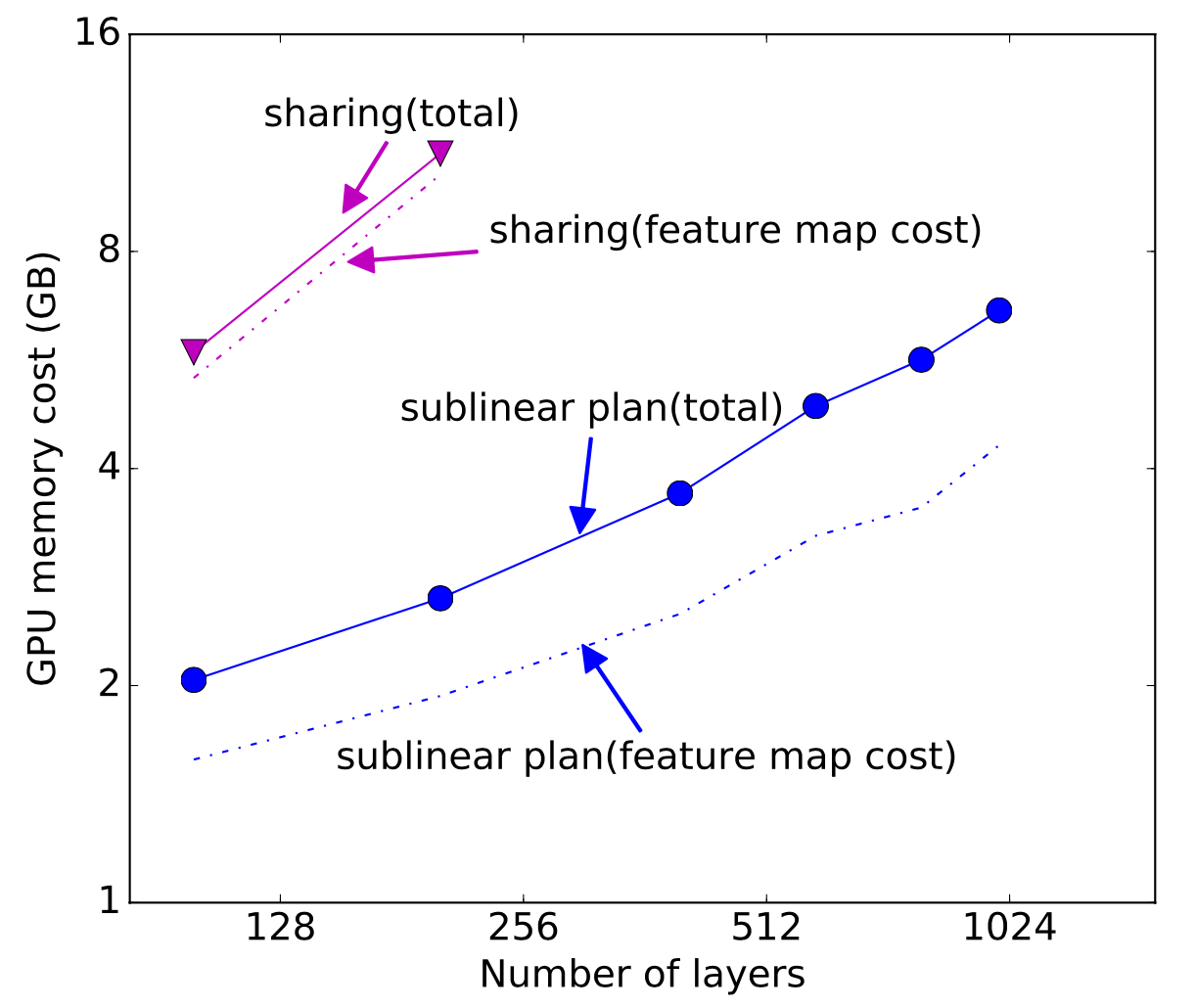
可以看出不使用本文提出的计算换内存的方法,最多只能训练200+层的网络,而使用本文提出的算法后可以训练1000+以上层数的网络,极大地增加了GPU可以训练的模型范围。
下图展示了节省存储所需的额外计算开销情况:
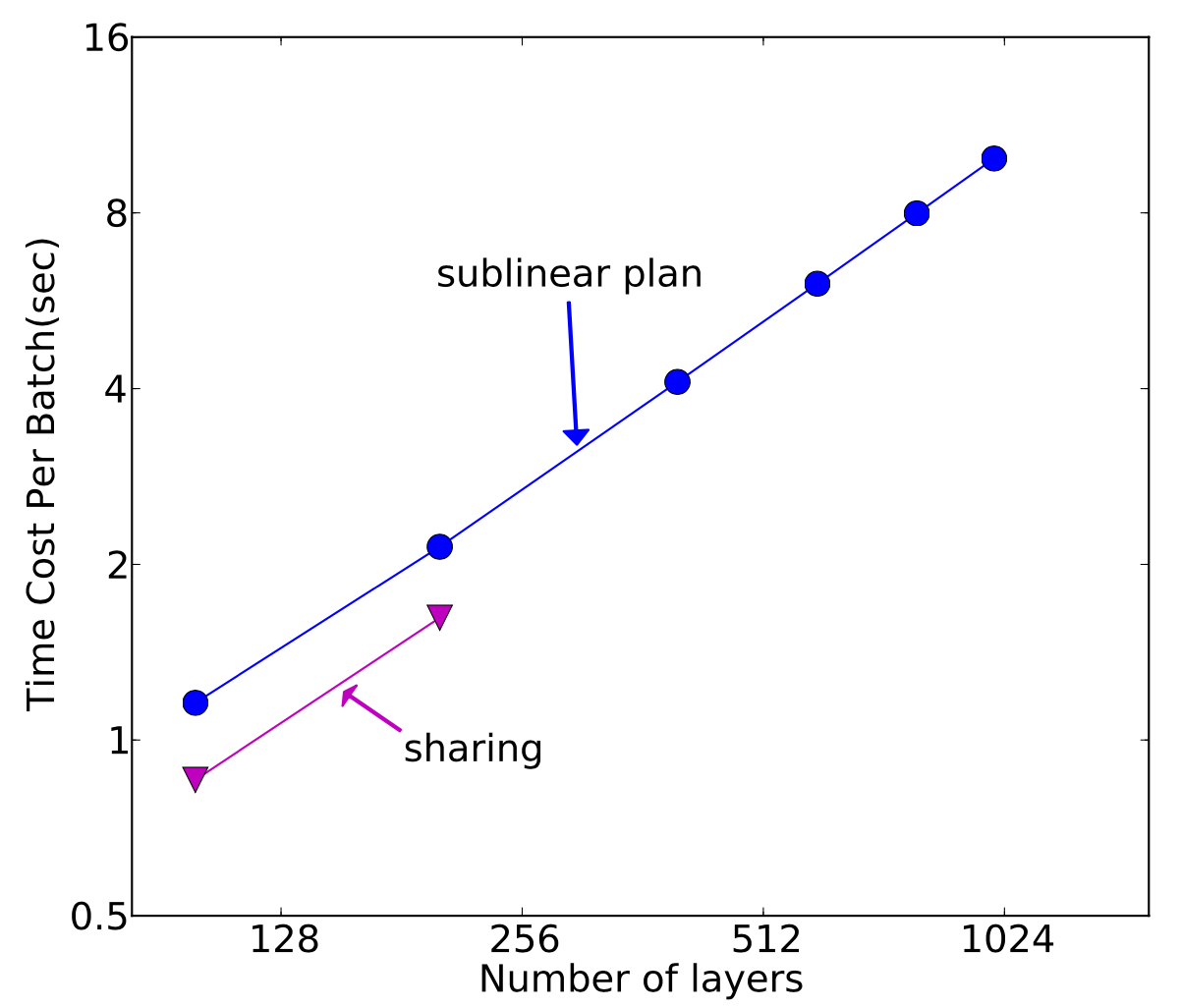
可以看到,本文提供的方法大概增加了30%的计算时间,这在很多无法训练大模型的情况下显然是可以接受的。
其它
关于内存优化的更多信息,大家可以查看相关论文,同时有一篇非常好的博客可以参考[2]。
引用
[1] Chen, Tianqi, et al. "Training deep nets with sublinear memory cost." arXiv preprint arXiv:1604.06174 (2016).
[2] Fitting larger networks into memory. https://medium.com/tensorflow/fitting-larger-networks-into-memory-583e3c758ff9

更多推荐