
文章目录
译著:这篇文章翻译自:https://lilianweng.github.io/lil-log/2021/12/05/semi-supervised-learning.html。感谢lilianweng 的幸苦工作。
简介在监督学习中,高质量的标签是任务性能的保障。然而,给大量的数据样本打标签的代价是非常昂贵的。由此,机器学习中诞生了一些新的范式,专门用于解决在标签非常缺乏的情况下的学习问题。在这些范式中,半监督学习是一个可选方案(半监督学习仅需依赖很少部分打过标签的数据+大量无标签数据)。
在监督学习任务中,如果我们仅有少量的带标签数据,通常我们会考虑以下四个方法:
- 预训练+微调:在一个非常大的非监督数据集上进行任务无关的模型训练,比如:使用纯文本训练的预训练语言模型,通过自监督学习对无标签图片训练的预训练视觉模型。得到预训练模型之后,我们再将预训练模型在下游任务上,使用少量的带标签数据进行微调
- 半监督学习:从有标签和无标签样本中一起学习。许多视觉任务的研究都属于此范围
- 主动学习 (Active learning):虽然打标签代价较大,但此项工作我们一般仍会有一定的预算。我们可以使用主动学习来将预算的效用最大化。主动学习的目的是选出那些最有价值的无标签样本,以用于下一步的标签采集工作
- 预训练+自动生成数据集:给定一个好的预训练模型,我们可以用它来自动生成更多标记的样本来。在*小样本学习 (few-shot learning)*成功之后,这个方法语言领域非常流行
我计划写一个关于“在没有足够数据情况下学习”的系列文章,本文是其中的第一部分,是关于半监督学习的。
什么是半监督学习?
半监督学习既使用有标签数据,也使用无标签数据进行模型训练。
有趣的是,在当前的学术研究中,大多数半监督学习都聚焦于视觉任务上。而预训练+微调的方法则是语言任务中常用的方法。
这篇文章中介绍的所有方法中使用的损失函数都由两部分构成:$\mathcal{L} = \mathcal{L}_s + \mu(t) \mathcal{L}_u$。其中,$\mathcal{L}_s$为监督学习的部分,它在给定样本标签的情况下很容易得到。此处,我们主要关注非监督损失函数$\mathcal{L}_u$的设计。损失函数中权重函数$\mu(t)$常被设计为:随着训练时间$t$的推移来增加非监督损失$\mathcal{L}_u$的权重。
声明:这篇文章不会包含哪些关注模型改动的半监督学习方法。查看这篇综述来了解如何在半监督学习中使用生成模型和基于图的方法。
符号说明
| 符号 | 说明 |
|---|---|
| $L$ | 不同标签的数量 |
| $(\mathbf{x}^l, y) \sim \mathcal{X}, y \in \{0, 1\}^L$ | 标记好的数据集;$y$是标签的 one-hot 编码 |
| $\mathbf{u} \sim \mathcal{U}$ | 无标签数据集 |
| $\mathcal{D} = \mathcal{X} \cup \mathcal{U}$ | 包含带标签和无标签的整个数据集 |
| $\mathbf{x}$ | 任意样本(有标签或无标签) |
| $\bar{\mathbf{x}}$ | 数据增强样本 |
| $\mathbf{x}_i$ | 第$i$个样本 |
| $\mathcal{L},\mathcal{L}_s,\mathcal{L}_u$ | 损失函数,监督损失函数,非监督损失函数 |
| $\mu(t)$ | 非监督损失权重,随时间单调不减 |
| $p(y \vert \mathbf{x}), p_\theta(y \vert \mathbf{x})$ | 给定输入样本$x$,标签的条件概率分布 |
| $f_\theta(.)$ | 待训练的神经网路模型,参数为$\theta$ |
| $\mathbf{z} = f_\theta(\mathbf{x})$ | $f$输出的 logits 向量 |
| $\hat{y} = \text{softmax}(\mathbf{z})$ | 预测标签的概率分布 |
| $D[.,.]$ | 测量两个分布的距离函数,比如:MSE/交叉熵/KL散度 |
| $\beta$ | EMA权重超参数(用于teacher模型) |
| $\alpha, \lambda$ | MixUp的参数,$\lambda \sim Beta(\alpha, \alpha)$ |
| $T$ | 用于调节预测分布的温度参数 |
| $\tau$ | 用于选择输出预测的置信阈值 |
假设
学术研究中使用了一些假设来支撑半监督学习方法的设计:
- H1:平滑性假设:如果两个样本在特征空间的高密度区域很接近,那么它们的标签也应该相似或者一样
- H2:集群假设:特征空间包含高密度区域和稀疏区域。高密度区域自然聚集为一个群,同一个群中的样本被期望属于同一个标签。该假设为$H1$的一个扩展
- H3:低密度可分假设:不同类别数据的决策边界应该在特征空间的稀疏区域,否则决策边界会将一个高密度区域分为两个类别,这就违背了$H1$和$H2$
- H4:流形假设:高维数据可以映射到一个低维的流形(manifold)上。虽然,我们在现实世界所观察到的数据,它们的维度可能非常高(例如:现实世界一些物体/场景的图片),但是实际上它们可以被一个低维的流形捕获。在高维空间中相似的点映射到低维空间后,它们之间的距离仍然相近,我们依然可以据此对这些相似数据进行分组(举例:现实世界的图片的像素点显然不是一个在所有像素点上的均匀分布,它们是有一定规律的)。该假设让我们对高维数据学习一个更加高效的低维表征成为可能。我们可以直接在低维空间中测量无标签数据点之间的相似度。这也是表征学习的基础。【查看此链接了解更多】。
一致性正则 (Consistency Regularization)
一致性正则(通常也称作一致性训练)假设:对于同样的输入,神经网络内部的随机性(比如通过dropout)或者数据增强变换,不应该改变模型的输出预测。本章节中的每个方法都使用了一致性正则损失,记为$\mathcal{L}_u$。
一致性正则的思想已经被许多的自监督学习方法所采纳,比如:SimCLR, BYOL, SimCSE等等。同一样本的不同数据增强版本所得到的表征应该是一样的。语言模型中的交叉视野训练(cross-view training)和自监督学习中的多视野学习 (multi-view learning)都基于同样的动机发展而来。
π 模型

Sajjadi 等人, (2016)提出了一个新的非监督学习损失函数,该损失函数用于最小化同一样本的不同增强版本经过网络变换(比如:dropout, 随机最大池化操作)处理后,它们之间的差异。该损失函数中标签数据没有被显式的使用,所以它可以被用到无标签数据集中。Laine & Aila (2017)等人为此模式起了一个名字叫π模型。
其中,$f'$是采用了不同数据增强策略或者不同dropout的结构一样的神经网络;$\mathcal{D}$为整个数据集。
分时聚合(Temporal ensembling)

π模型要求模型每次对单个样本运行两次运算,这样就将计算量加倍了。为了降低计算成本,分时聚合(Laine & Aila 2017)方法对每个训练样本$\tilde{\mathbf{z}}_i$维护了一个预测值的指数滑动平均(Exponential Moving Average, EMA)作为学习目标,这个值每一轮(epoch)只会被求值和更新一次。由于聚合输出$\tilde{\mathbf{z}}_i$的初始值被设置为$0$,为$\tilde{\mathbf{z}}_i$引入了偏差。为了消除这个偏差,这里使用系数$(1-\alpha^t)$对其进行修正。Adam优化器中出于同样的原因也使用了此偏差修正项。
其中$\tilde{\mathbf{z}}^{(t)}$是第$t$轮的聚合输出,$\mathbf{z}_i$是当前轮(round)的模型预测值。注意,由于$\tilde{\mathbf{z}}^{(0)} = \mathbf{0}$,这里$\tilde{\mathbf{z}}^{(1)}$(首轮值)就等于$\mathbf{z}_i$。
均值导师 (Mean Teachers)
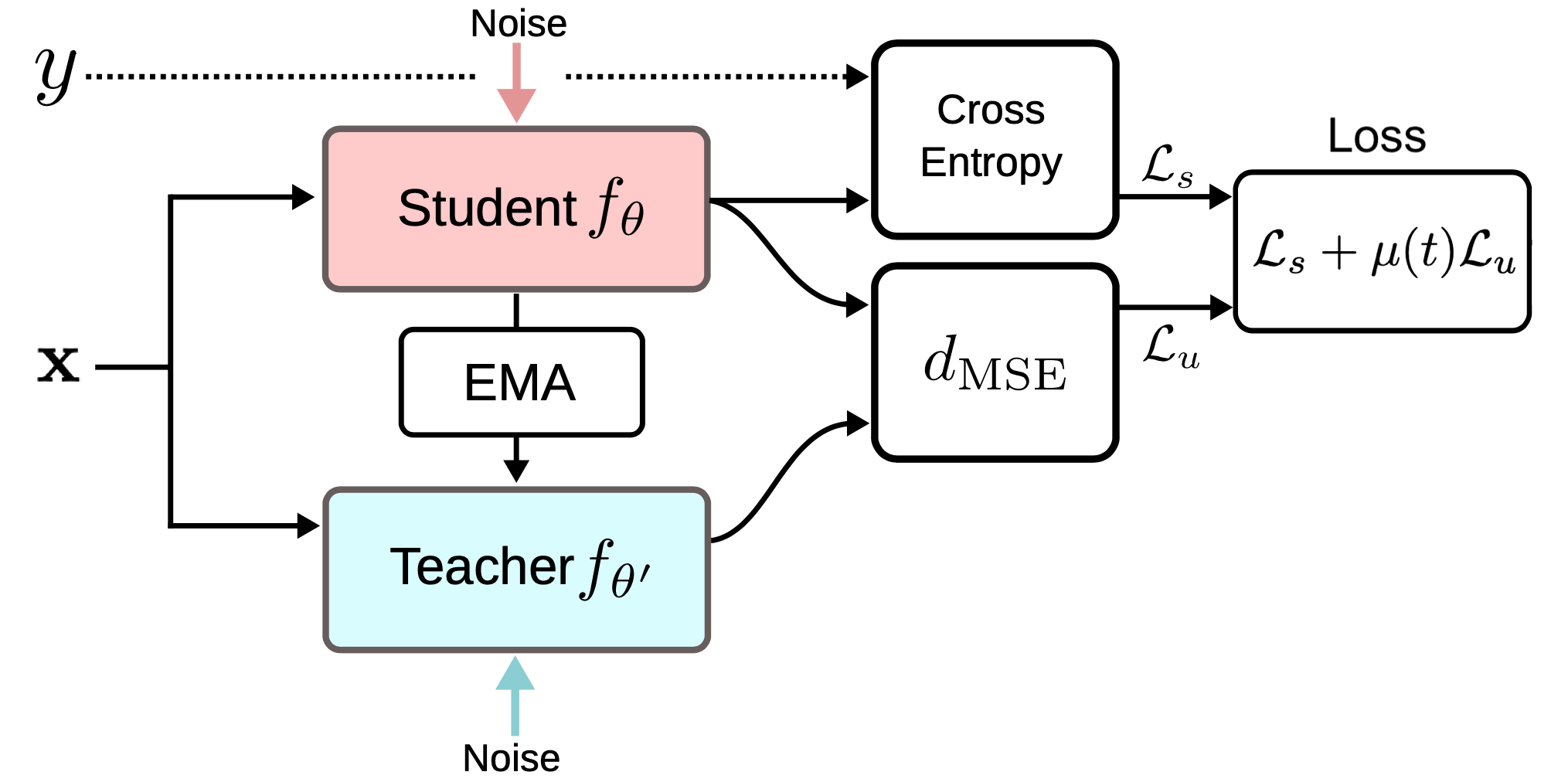
分时聚合中为每个训练样本记录了标签预测的EMA值,并用它们作为训练目标。然而,该标签每轮(epoch)才会更新一次,当数据集非常大的时候,这个方法就显得很笨拙。均值导师(Tarvaninen & Valpola, 2017)的提出就是为了克服这个更新缓慢的缺点。该方法通过跟踪模型权重值的滑动平均而非模型的输出来达到这个目的。我们称带参数$\theta$的原始模型为学生模型(student model),学生模型权重值的滑动平均值记为$\theta'$,使用此参数的模型我们称之为均值导师模型(mean teacher model):$\theta’ \gets \beta \theta’ + (1-\beta)\theta$。
一致性正则损失就是学生模型和导师模型预测值之间的距离,也就是我们希望最小化的目标。我们期望均值导师模型可以提供相比于学生模型更加准确的预测值。根据经验,从实验结果来看,这一点被证实了。几种方法的对比参考下图。
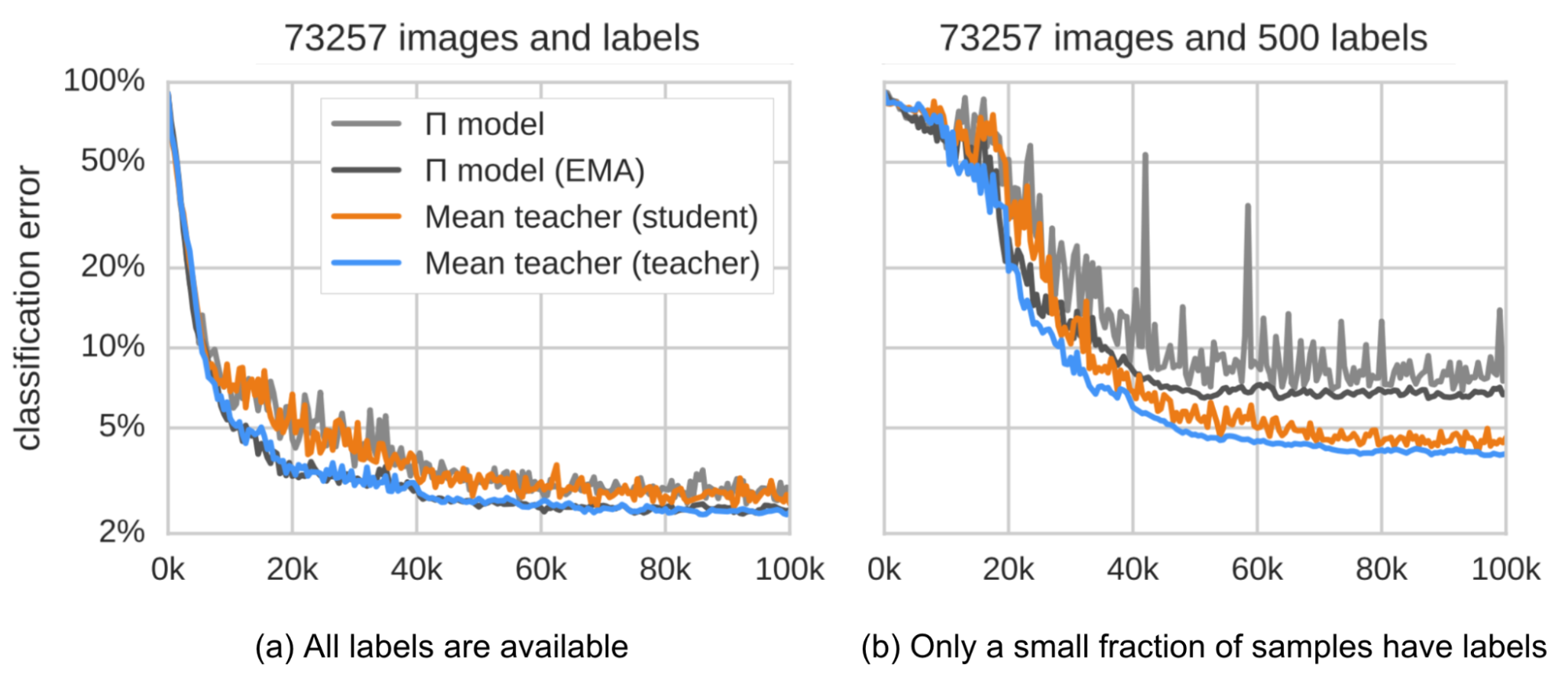
根据他们的对比实验(ablation studies):
- 输入增强(比如:输入图片随机翻转、加入高斯噪声)以及学生模型的dropout对于性能提升是必要的。Dropout在导师模型中不是必要的
- 性能表现对于EMA的衰减参数$\beta$很敏感。一个比较好的策略是:在“下坡阶段”使用一个较小的$\beta=0.99$,而在后续学生模型已经较为稳定阶段使用一个较大的$\beta=0.999$
- 作为一致性损失函数,MSE的表现相比于其它损失函数(比如:KL散度)要好
使用噪声样本作为学习目标
最近的一些一致性训练方法将训练目标设置为:最小化原始无标签样本与其对应的增强样本之间的距离。这和π模型非常相似,但是它们的一致性损失函数仅去计算无标签数据。
对抗训练(Adversarial Training)(Goodfellow 等人,2014)给输入加上对抗噪声来让训练出的模型更加鲁棒。该设置适用于监督学习,
其中,$q(y \mid \mathbf{x}^l)$为真实分布,它使用真实标签$y$的one-hot编码来近似;$p_\theta(y \mid \mathbf{x}^l)$为模型给出的预测分布;$D[.,.]$是测量两个分布之间距离的函数。
虚拟对抗训练(Virtual Adversarial Training, VAT;Miyato 等人, 2018)将这个思想拓展到半监督学习中去。由于(在半监督学习中)$q(y \mid \mathbf{x}^l)$是未知的,VAT使用当前模型(参数为$\hat{\theta}$)的预测作为替代。注意,$\hat{\theta}$仅为当前模型的一个拷贝,它不会被更新。
VAT损失函数适用于带标签和不带标签的数据。它是当前模型在每一个数据点上的预测流形的负平滑度的度量。优化此损失函数可以让流形更加的平滑。
插值一致性训练(Interpolation Consistency Training, ICT;Verma 等人, 2019)通过给数据点添加更多的插值来增强数据集,并期望模型的预测值与相应的插值标签一致。Mixup(Zheng等人, 2018)操作将两张图片通过简单的加权求和来混合两个图像,并将其与标签平滑相结合。和Mixup的思想一致,ICT期望模型对混合样本的预测可以与相应输入样本(用于混合的样本)标签的预测的插值相匹配,也就是:

上图中$\theta^\prime$是参数$\theta$的滑动平均(作为均值导师)。
由于随机选择的两个样本属于不同类别的概率还是比较大的(比如:Image Net数据集中有1000个类别),这样产生的插值样本很可能正好处于两个(不同)类别的决策边界上。根据我们前文描述的低密度可分假设,决策边界往往位于低密度区域。
其中$\theta^\prime$是$\theta$的滑动平均。
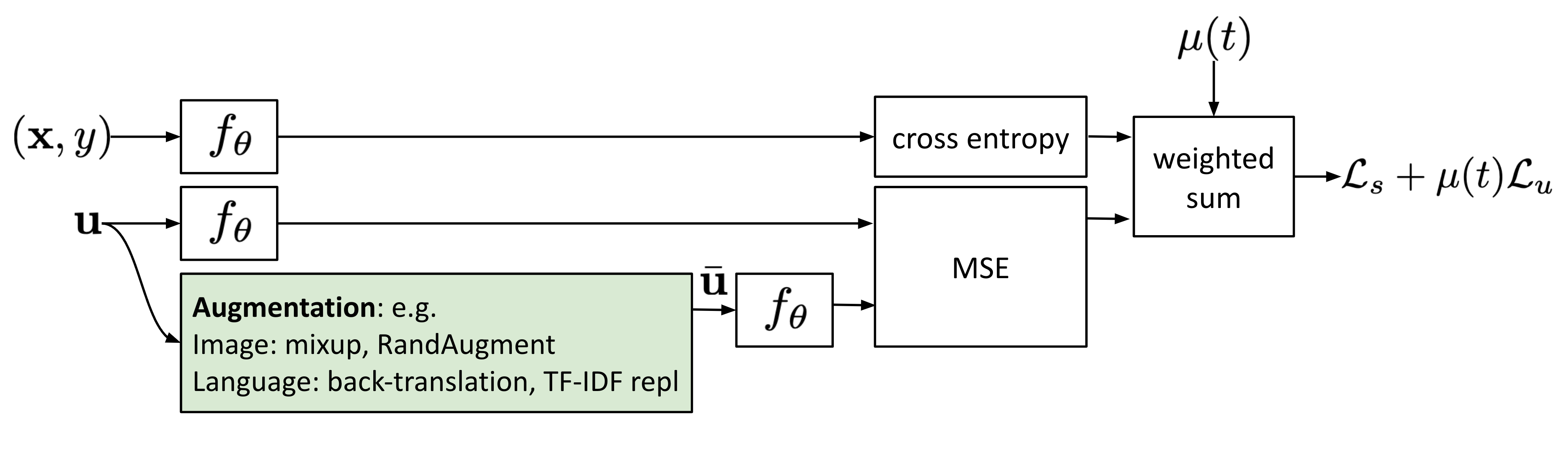
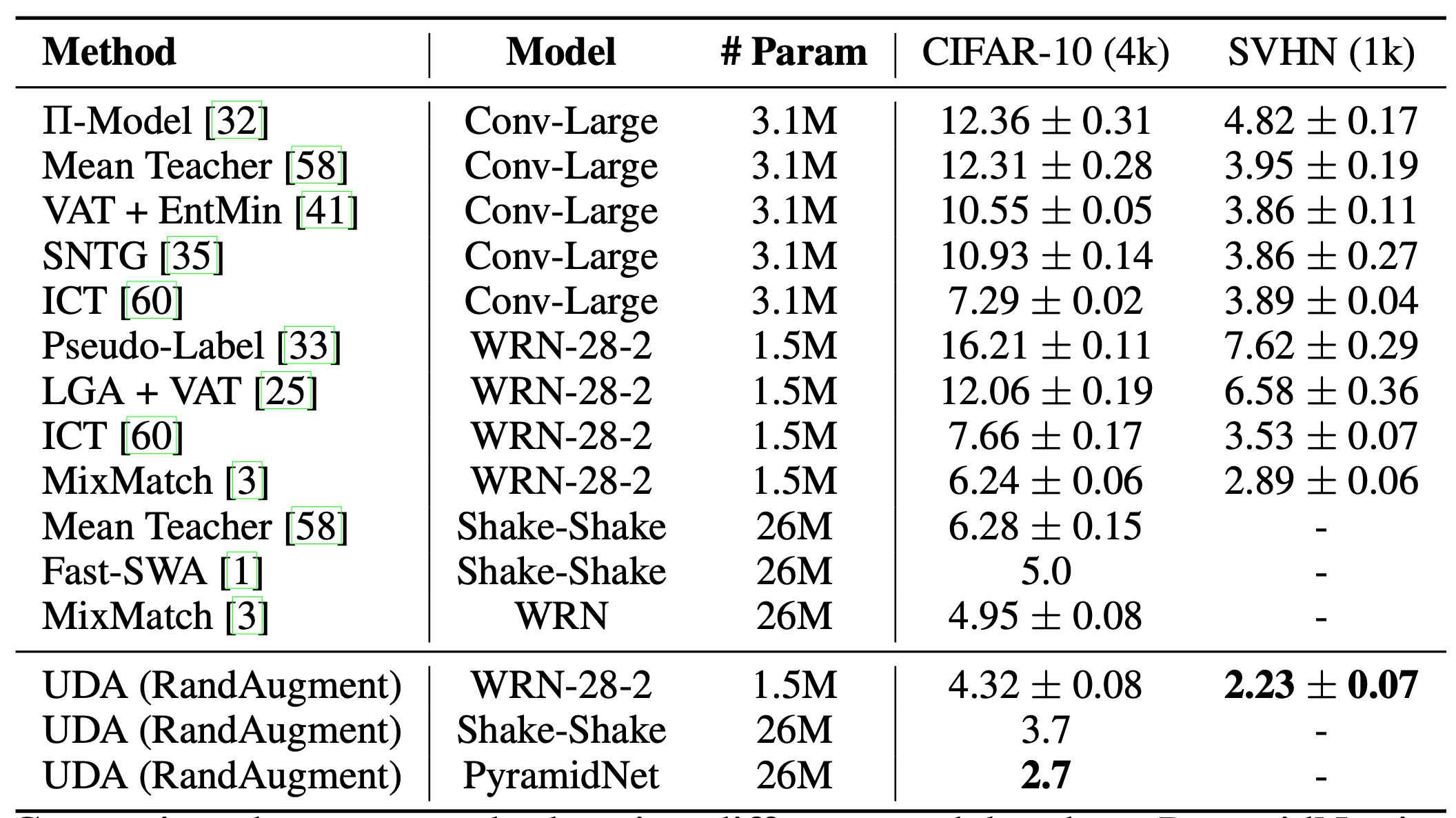
类似VAT,非监督数据增强(Unsupervised Data Augmentation, UDA;Xie等人, 2020)期望模型对于原样本(无标签)与增强样本给出同样的标签预测。UDA特别侧重于研究不同质量的噪声是如何影响半监督一致性训练的性能的。使用先进的数据增强方法来产生有意义且有效的噪声样本对于最后性能的影响举足轻重。好的数据增强方法可以生成有效而(也就是不会改变样本原本的标签)多样性的噪声,并且带有针对性的归纳偏置。
对于图片来说,UDA中应用了随机增强(RandAugment;Cubuk 等人, 2019)算法。随机增强算法对于PIL库中提供的数据增强操作进行随机均匀采样,无需学习或者优化。因此它相比于AutoAugment,代价极低。
对于语言任务来说,UDA将回译(back-translation)与基于TF-IDF的单词替换相结合。回译可以保持句子的高层语义,但是回译后句子所用单词很可能与原本句子中使用的并不一样;而基于TF-IDF的单词替换会删除TF-IDF分数较低的无信息单词。在语言任务的实验中,他们发现UDA可以用作迁移学习和表征学习的补充;举例来说,将BERT在域内无标签数据上进行微调后可以进一步改善性能(下图中$\text{BERT}_\text{FINETUNE}$)。

计算$\mathcal{L}_u$时,UDA发现了三个改善训练的技巧:
- 低置信度掩弃:将低预测置信度(小于阈值$\tau$)的样本丢掉
- 锐化预测分布:使用较低的softmax的温度来锐化概率分布
- 域内数据过滤:为了从一个非常大的域外数据中提取更多的域内数据,他们训练了一个分类器用于预测域内标签,将置信度高的样本作为候选域内样本
其中$\hat{\theta}$为模型参数的一个固定的拷贝(和VAT中一样,梯度不更新),$\bar{\mathbf{x}}$为数据增强版本,$\tau$为预测置信度的阈值,$T$为锐化softmax函数的温度值。
伪标签
伪标签(Lee 2013)使用当前模型给无标签的样本打上标签,然后将所有样本当作为全监督学习的数据集进行训练。
为什么伪标签可以工作?伪标签实际上相当于熵正则化(Grandvalet & Bengio 2004),它最小化了无标签数据的类别概率的条件熵,这有利于不同类别在低密度区域分离。换句话说,预测得到的类别概率实际上是类重叠的一个度量,最小化熵相当于降低类别重叠,从而保证低密度可分。
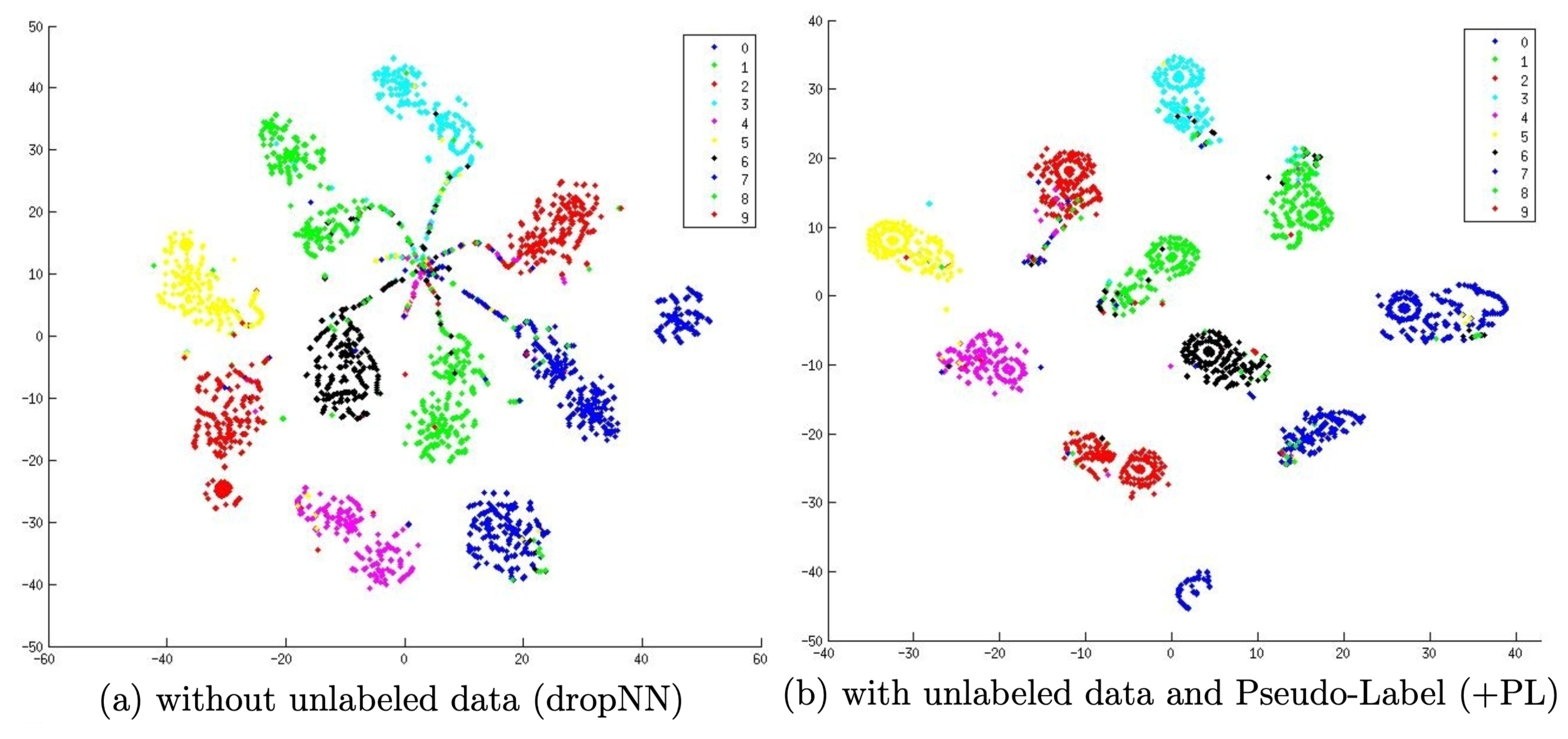
使用伪标签进行训练的过程显然应该是一个迭代的过程。我们将产生伪标签的模型成为导师模型(teacher),而将学习伪标签的模型成为学生模型(student)。
标签传播
标签传播(Iscen 等人, 2019)通过样本的特征嵌入来构建相似性图。然后标签从已知标签的样本“扩散”到未知标签的样本。传播权重与图中节点对的相似度成正比。从概念上讲,这类似于knn分类器,并且它们都有扩展性问题。
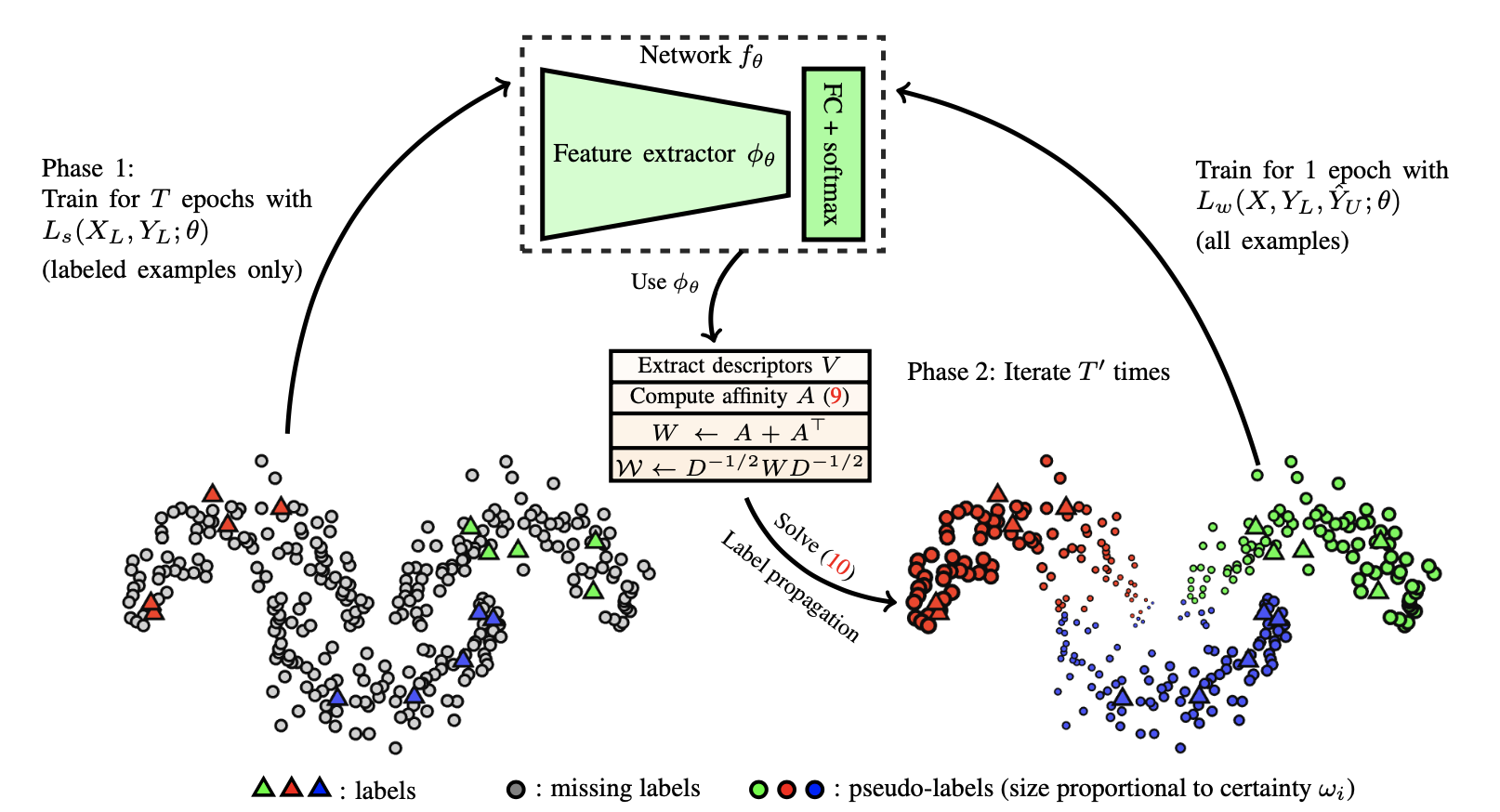
自训练
自训练不是一个新的概念(Scudder 1965,Nigram & Ghani CIKM 2000)。这是一种迭代算法,它会循环执行两个步骤,直到给无标签数据打完标签为止:
- 使用已有标签的数据集训练一个分类器
- 使用训练好的分类器给无标签数据预测标签,将那些预测置信度最高的一些数据加入已标记数据集
Xie 等人, 2020在深度学习中应用了自训练,并且取得了极大的成果。在ImageNet分类任务上,他们首先训练了一个EfficientNet(Tan & Le, 2019)模型作为导师模型来为300M无标签的图片生成伪标签。然后,训练一个更大的学生EfficientNet模型来学习新的数据集(包含真实标签数据和伪标签数据)。他们设定中一个非常重要的点是:学生模型在学习过程中是加入噪声的,而导师模型生成伪标签的过程中是不加噪声的。因此,他们的方法又叫Noisy Student。实验中使用的添加噪声的方法包括:随机深度(Huang 等人, 2016)、dropout 和 RandAugment。添加的噪声会带来复合效应,可以让模型在决策边界更加平滑(包括标签数据和无标签数据)。这也是学生模型会比导师模型表现更好的原因。
学生模型训练中其它一些重要的技术点:
- 学生模型必须足够大(比导师模型大),以拟合更多的数据
- 噪声学生(Noisy Student)模型的训练应当采用数据平衡策略(data balancing),特别是在每个类别标签的数据中去平衡伪标签数据的数量
虽然,噪声学生模型不是专门为了对抗攻击而设计的,但是它也改善了抵御 FGSM(Fast Gradient Sign Attack:此攻击损失函数梯度来调整输入数据以最大化损失)的能力。
SentAugment(Du 等人, 2020)方法旨在解决在语言领域中,没有足够域内标签数据情况下的一些问题。它依赖使用句子嵌入来从一大堆无标签语料中去寻找域内数据,而后使用得到的句子进行自训练。
降低确认偏差
确认偏差指的是:由于导师模型并不是完美的,因此,它给出的标签无法保证完全正确。如果我们在训练学生模型的过程中去拟合错误的标签,那显然我们无法得到一个非常好的模型。
为了降低确认偏差,Arazo 等人 (2019)提出了两个技术。一个是使用带软标签的MixUp。给定两个样本$(\mathbf{x}_i, \mathbf{x}_j)$和对应的真实或者伪标签$(y_i, y_j)$,那么我们可以使用插值标签的方式来计算交叉熵损失(用softmax的输出):
如果我们仅有极少量的已标记数据,那么仅用Mixup方法还不够。他们通过采样(oversampling)来保证在每一个mini-batch中已标签样本的数量至少要达到一个下限阈值。这种方法要比提高已标记数据的权重要好,因为它是去提高更新频率而不是去提高更新幅度(提高更新幅度可能会导致训练不稳定)。和一致性正则类似,数据增强和dropout对于伪标签也工作的很好。
元伪标签(Meta Pseudo Labels, Pham 等人, 2021)通过学生模型在已标记数据上表现的反馈来不断调整导师模型。学生模型与导师模型并行训练,其中学生模型从伪标签中学习,导师模型学习如何打伪标签。
记$\theta_T, \theta_S$分别为导师模型和学生模型的参数。学生模型在已标记样本上的损失定义为$\theta_T$的函数$\theta_S^{PL}(.)$。我们希望通过优化导师模型来相应的优化此损失函数。
然而,直接优化上面的等式是不可行的。此处借用MAML的思想,我们可以使用$\theta_S$的单步梯度更新来近似多步的$\arg \min_{\theta_S}$,
如果使用软伪标签,上面的目标函数是可微的。但是如果使用硬伪标签,上面的式子就是不可微的。所以我们需要使用 RL(比如 REINFORCE)。
优化过程在两个模型的训练中交替进行:
- 学生模型的更新:给定一批无标签样本$\{ \mathbf{u} \}$,我们通过$f_{\theta_T}(\mathbf{u})$来生成伪标签,通过单步SGD来优化$\theta_S$:$\theta’_S = \color{yellowgreen}{\theta_S - \eta_S \cdot \nabla_{\theta_S} \mathcal{L}_u(\theta_T, \theta_S)}$
- 导师模型的更新:给定一批已标记样本$\{(\mathbf{x}^l, y)\}$,我们重用学生模型的更新进行$\theta_T$的优化:$\theta’_T = \theta_T - \eta_T \cdot \nabla_{\theta_T} \mathcal{L}_s ( \color{yellowgreen}{\theta_S - \eta_S \cdot \nabla_{\theta_S} \mathcal{L}_u(\theta_T, \theta_S)} )$。此外,这里导师模型中,无标签数据的一致性正则使用了UDA目标函数
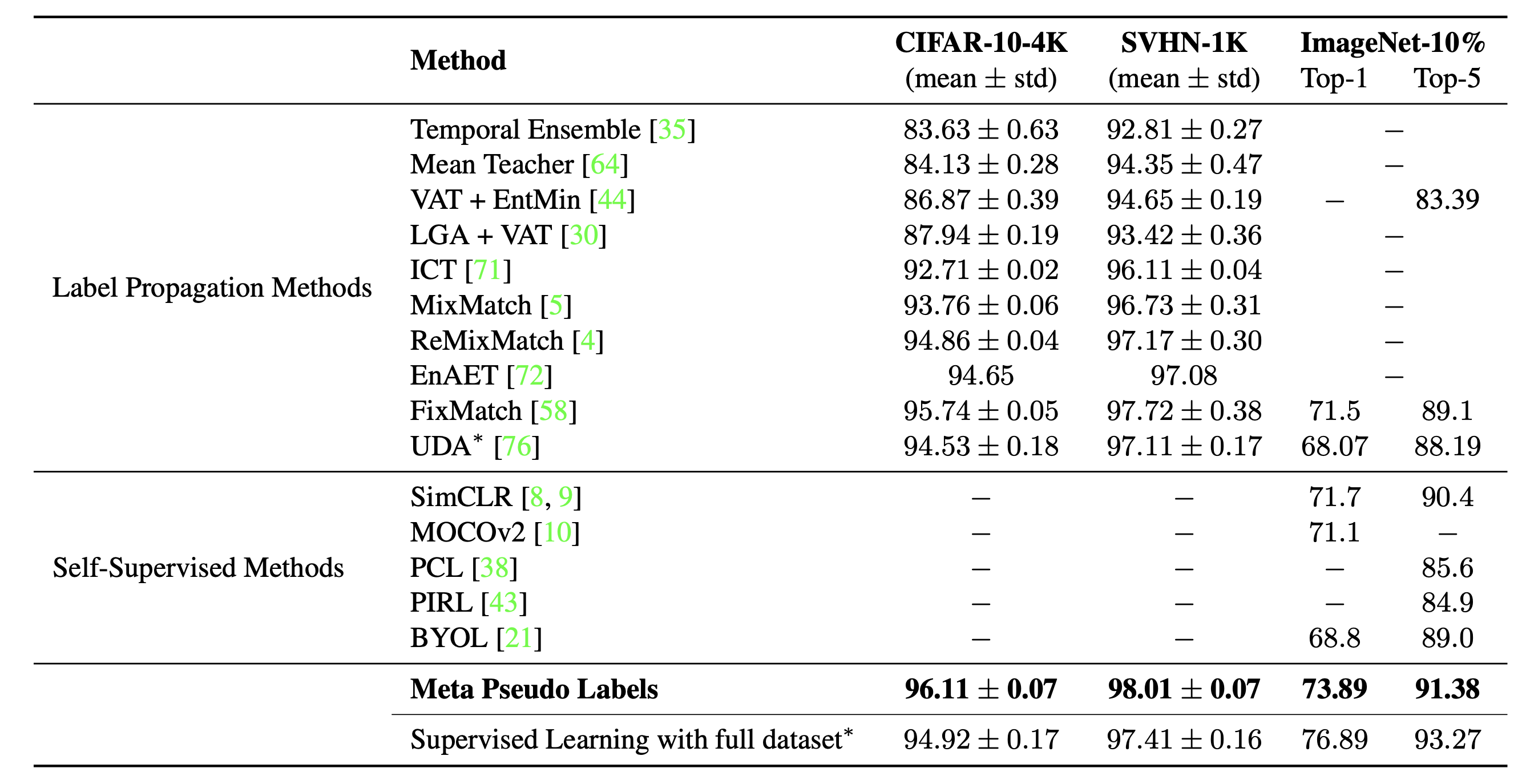
伪标签+一致性正则
在半监督学习中将伪标签和一致性训练结合起来是可能的。
MixMatch
MixMatch(Berthelot 等人, 2019)作为半监督学习中一个较为完善的方法,为了利用无标签数据,它将以下技术结合起来:
- 一致性正则:让模型对经过扰动的样本输出与原样本同样的预测
- 熵最小化:让模型对于无标签数据输出高置信度的预测
- MixUp增强:让模型在样本间有线性的行为表现
给定一批带标签数据$\mathcal{X}$和无标签数据$\mathcal{U}$,我们通过$\text{MixMatch}(.)$来创建它们的增强版本$\bar{\mathcal{X}}, \bar{\mathcal{U}}$,它们包含了增强后的样本以及无标签样本的猜测标签。
其中$T$为锐化温度参数,用于降低猜测的标签间的重叠度;$K$表示给每个无标签样本生成的增强版本的数量;$\alpha$是MixUp的参数。
对于每个无标签样本$\mathbf{u}$,MixMatch生成$K$个增强版本$\bar{\mathbf{u}}^{(k)} = \text{Augment}(\mathbf{u}), k=1, \dots, K$,伪标签的猜测使用均值:$\hat{y} = \frac{1}{K} \sum_{k=1}^K p_\theta(y \mid \bar{\mathbf{u}}^{(k)})$。

根据他们的对比研究,在无标签数据上使用MixUp极为重要;将伪标签分布的锐化操作去掉会在很大程度上影响最终性能;在标签猜测中,使用多个增强版本的均值也是很有必要的。
ReMixMatch(Berthelot 等人, 2020)在MixMatch的基础上引入了下面两个新的机制以改进其性能:

- 分布对齐:此机制鼓励边缘分布$p(y)$与真实标签的边缘分布靠近。令$p(y)$为真实类别的分布,$\tilde{p}(\hat{y})$为在无标签样本上得到的预测类别分布,那么模型给出的无标签样本的预测会进行归一化操作:$\text{Normalize}\big( \frac{p_\theta(y \vert \mathbf{u}) p(y)}{\tilde{p}(\hat{y})} \big)$,以便匹配真实的边缘分布。
- 注意,如果边缘分布不是均匀分布,那么熵最小化不是有用的目标函数
- 我真的认为无标签数据和有标签数据的分布相匹配这个假设太强了,现实世界可能不成立
- 增强锚点:给定一个无标签样本,它首先使用弱增强策略生成一个锚点版样本。然后,我们使用CTAugment (Control Theory Augment) 来平均$K$个强增强版本。CTAugment 仅采样那些可以让模型预测保持在网络容差范围内的增强方法
ReMixMatch 损失函数由以下几部分构成:
- 使用数据增强和MixUp的监督损失
- 使用数据增强和MixUp的非监督损失(用伪标签作为目标)
- 在无标签图片的单个重度增强版上的交叉熵损失(不使用MixUp)
- 旋转损失(和自监督学习中的一样)
DivideMix
DivideMix(Junnan Li 等人, 2020)将半监督学习与噪声样本学习(Learning with Noisy Labels, LNL)结合起来。它通过高斯混合模型(GMM)对每个样本的损失分布进行建模,来动态地将训练数据划分为一个干净的带标签的集合和另一个无标签的噪声样本集合。根据论文Arazo 等人, 2019中的想法,他们使用单样本交叉熵损失函数$\ell_i = y_i^\top \log f_\theta(\mathbf{x}_i)$来训练一个二元GMM(two-component GMM)。干净的样本对应的损失应该下降地比噪声样本的要快。
均值较小的元(component)是对应干净样本的集群(cluster),我们用$c$来表示。如果GMM后验概率$w_i = p_\text{GMM}(c \mid \ell_i)$(也就是采样得到样本属于干净集合的概率)高于阈值$\tau$,样本被认为是一个干净的样本,否则认为它是噪声样本。我们称数据聚类这一步骤为联分(co-divide)。为了避免确认偏差,DivideMix同时训练两个网络,这两个网络都使用另一个网络生成的数据集划分。(参考 Double Q-learning)
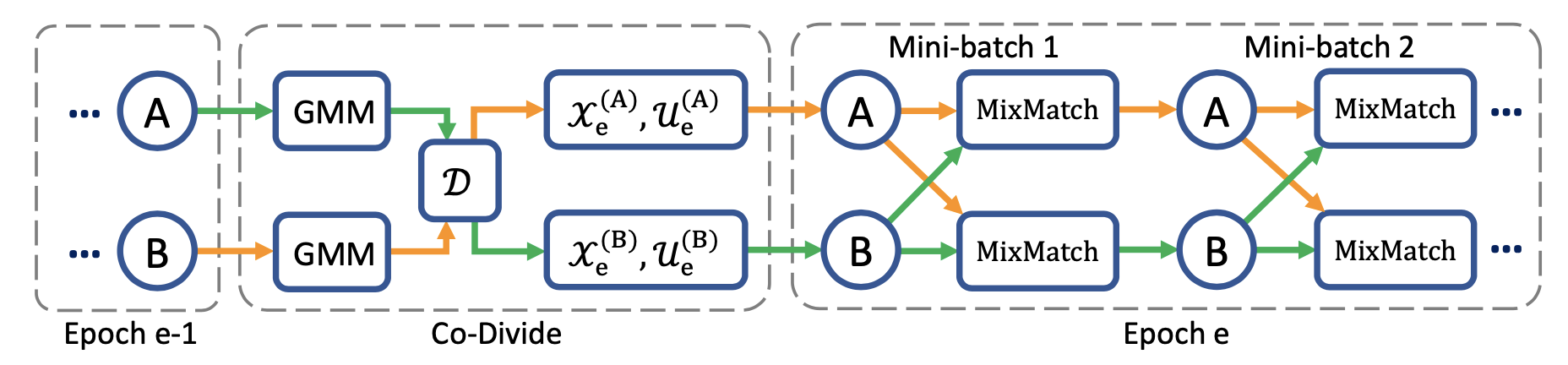
相比于MixMatch, DivideMix 有一个额外的联分环节用于处理噪声样本,同时它在训练时还有如下改进:
- 标签联调(co-refinement):将真实标签$y_i$与网络的预测$\hat{y}_i$进行线性组合,其中预测值$\hat{y}_i$是$\mathbf{x}_i$多个版本的增强样本预测的均值,这些预测值是另外一个网络给出的
- 标签联估(co-guessing):采用两个模型所给出预测的均值作为无标签样本的标签估计

FixMatch
FixMatch(Sohn 等人, 2020)使用弱增强方法来生成无标签数据的伪标签,并且它仅会保留高置信度的预测。这里弱增强方法和高置信度过滤都对生成高质量可信的伪标签很重要。而后,FixMatch 学习在给定一个重度增强样本的时候预测这些伪标签。
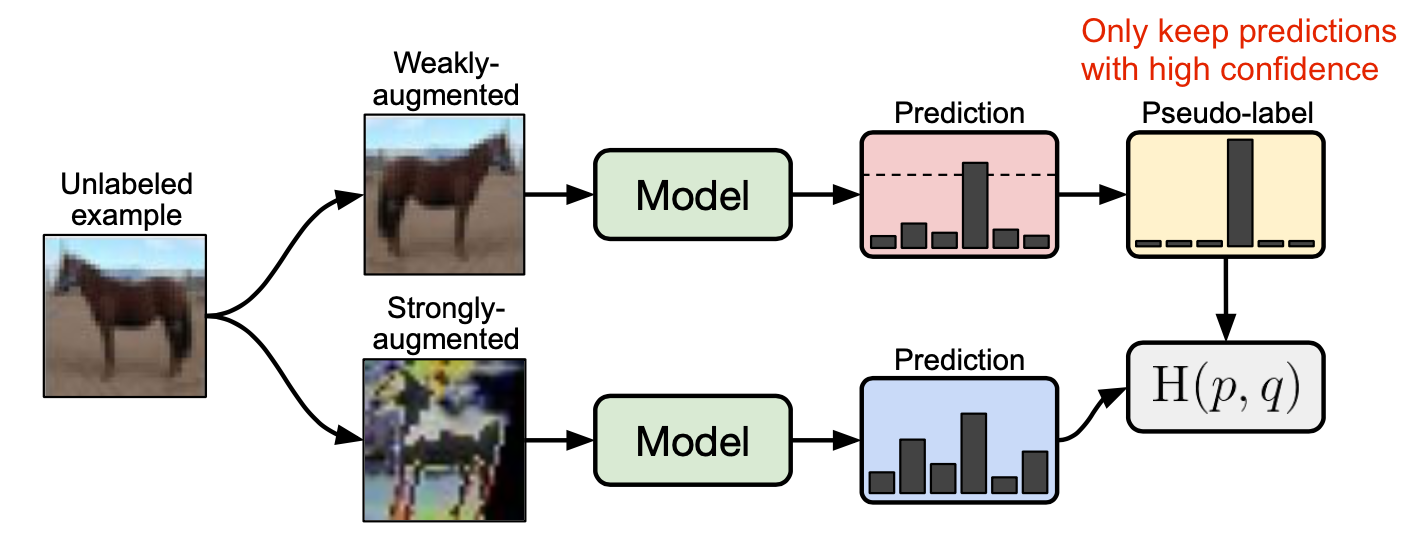
其中$\hat{y}_b$是无标签样本的伪标签;$\mu$是确定集合$\mathcal{X}, \mathcal{U}$相对大小的超参数。
- 弱增强$\mathcal{A}_\text{weak}(.)$:一个标准的反转移动增强
- 强增强$\mathcal{A}_\text{strong}(.)$:AutoAugment, Cutout, RandAugment, CTAugment

根据 FixMatch 的研究:
- 在使用阈值$\tau$的情况下,是否使用温度参数$T$来锐化预测的概率分布对结果影响不大
- 强增强方法中,Cutout 和 CTAugment 方法对性能影响较大
- 如果使用强增强方法替代弱增强方法进行伪标签估计,那么模型在训练早期就发散了。如果完全不使用弱增强方法,模型会过拟合于所猜测的标签(guessed labels)
- 如果使用弱增强方法替代强增强方法进行伪标签的预测,那么性能表现会不稳定。因此强数据增强方法非常重要
与预训练相结合
先在一大堆任务无关的数据集上训练一个预训练模型,而后再通过监督学习的方法将模型在下游任务上(使用较小的数据集)进行微调,已经成为一个常用的范式(特别是在语言相关的任务上)。研究表明,如果我们将预训练与半监督学习结合使用,那么我们会有额外的收益。
Zoph 等人, 2020研究了自训练可以在何种程度上工作得比预训练好。在实验中,他们使用ImageNet来进行预训练和自训练来改善COCO数据集的表现。注意他们在进行自训练的时候仅仅使用了ImageNet的图片数据,而未使用标签数据。He等人, 2018指出:使用ImageNet进行分类预训练在下游任务非常不同的时候(比如目标检测任务),效果不佳。
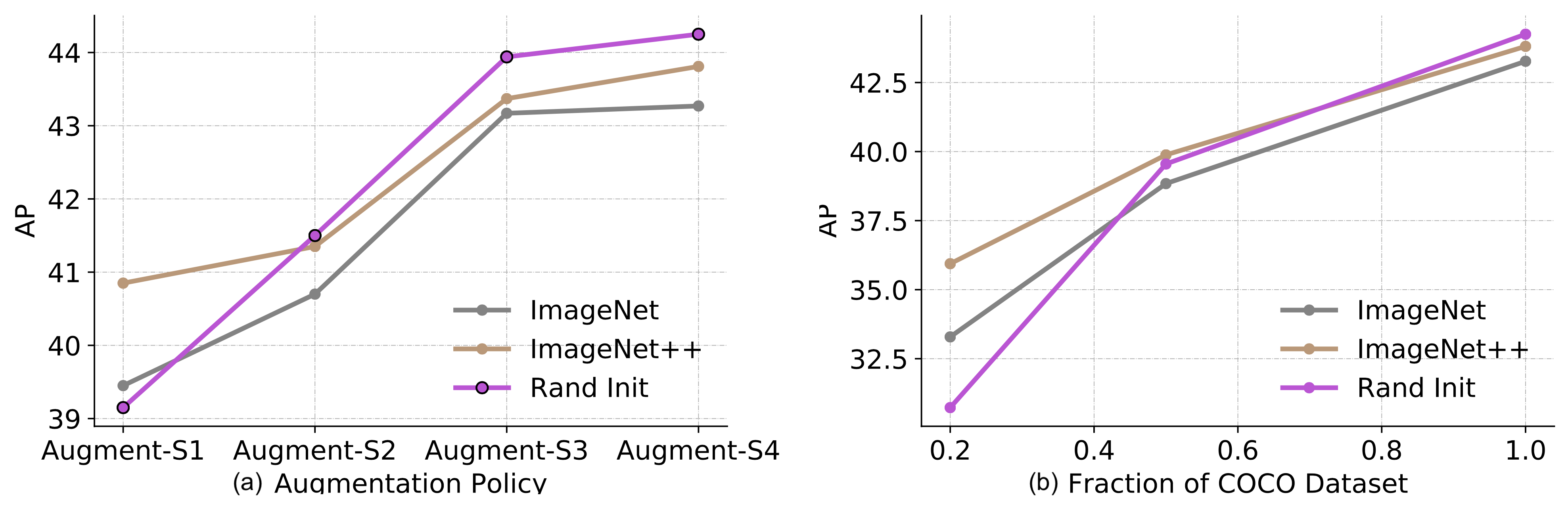
上图中,Rand Init表示模型使用随机权重进行初始化;ImageNet表示使用top-1准确率为84.5%的模型检查点进行初始化;ImageNet++表示使用一个更高的86.9%的准确率的检查点进行初始化。
他们的实验有一系列有趣的发现:
- 下游任务的带标签样本逐渐增多的时候,预训练带来的收益会逐渐消失。预训练在训练数据(带标签)较少的时候对性能改善是有帮助的,但是在数据量较多的时候预训练模型作用不大甚至会损害性能
- 如果使用强增强方法,即使预训练会损害性能,自训练仍然可以改善性能
- 即使使用同样的数据,自训练仍然可以在预训练的基础上改善性能
- 自监督预训练(比如使用SimCLR)会在数据量较多的情况下损害性能(和使用监督学习预训练一样)
- 联合训练(join-training)监督与非监督损失函数可以帮助解决预训练任务与下游任务之间的不匹配问题。预训练、联合训练以及自训练可以叠加
- 噪声标签以及无目标标签(un-targeted labeling, 也就是预训练数据的标签与下游任务的标签不匹配的情况)比不上有目的性的伪标签
- 自训练的计算代价比在预训练模型上进行微调的代价大
Chen 等人, 2020提出了一个三步过程来合并自监督预训练、监督微调和自训练:
使用非监督或监督学习来预训练一个大模型
在少量带标记的数据集上进行微调。这里使用一个很大(又深又宽)的神经网络很重要。在标签数据较少的时候,大模型可以带来更好的性能
通过自训练中的伪标签来对无标签数据进行知识蒸馏
- 由于特定任务无需使用到大的预训练模型给出的表征,所以将大模型进行知识蒸馏得到小模型是可能的
- 知识蒸馏使用的损失函数如下(其中导师模型的参数$\hat{\theta}_T$固定)
$$ \mathcal{L}_\text{distill} = - (1-\alpha) \underbrace{\sum_{(\mathbf{x}^l_i, y_i) \in \mathcal{X}} \big[ \log p_{\theta_S}(y_i \mid \mathbf{x}^l_i) \big]}_\text{监督损失} - \alpha \underbrace{\sum_{\mathbf{u}_i \in \mathcal{U}} \Big[ \sum_{i=1}^L p_{\hat{\theta}_T}(y^{(i)} \mid \mathbf{u}_i; T) \log p_{\theta_S}(y^{(i)} \mid \mathbf{u}_i; T) \Big]}_\text{无标签数据的蒸馏损失} $$
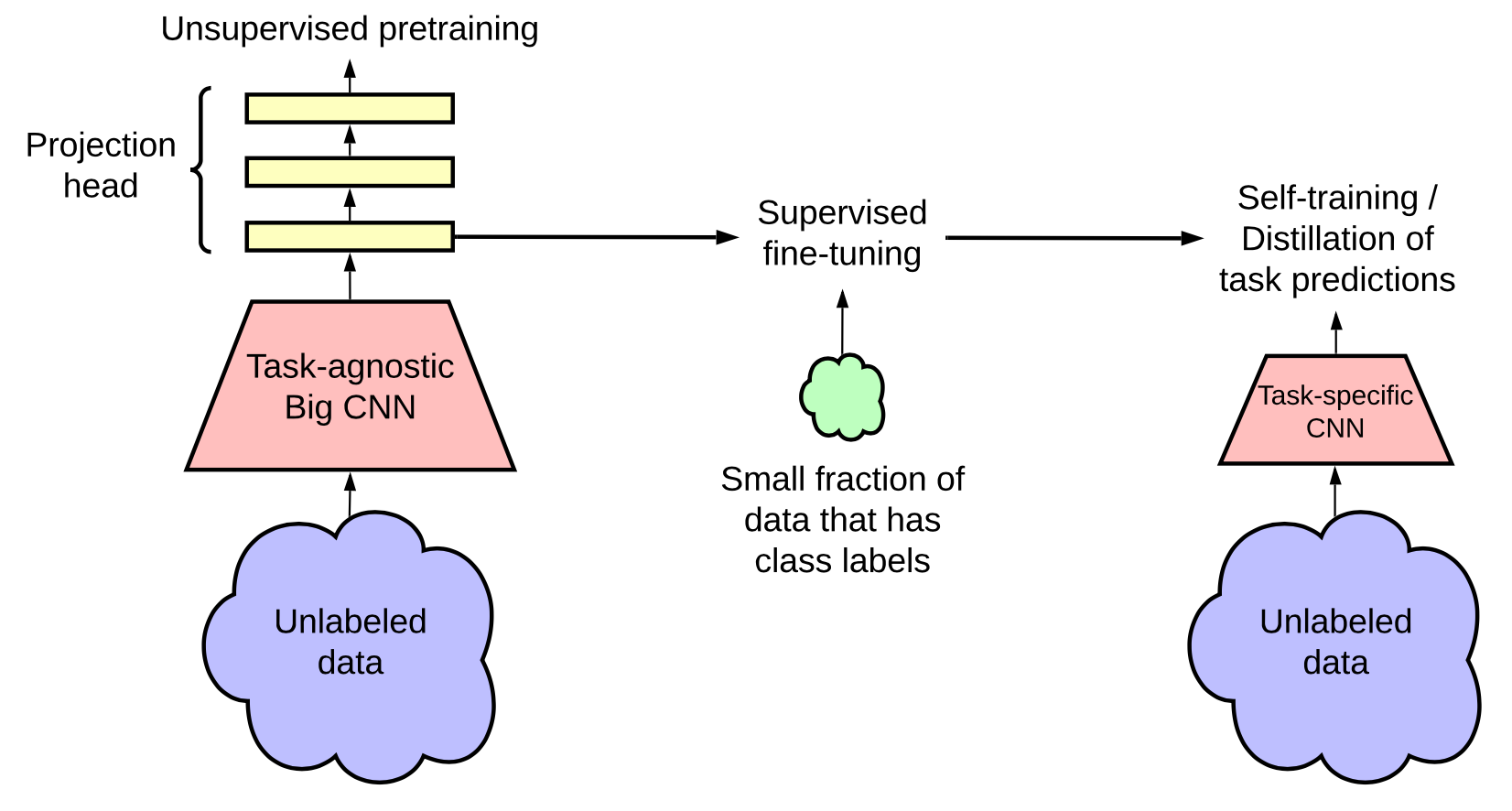
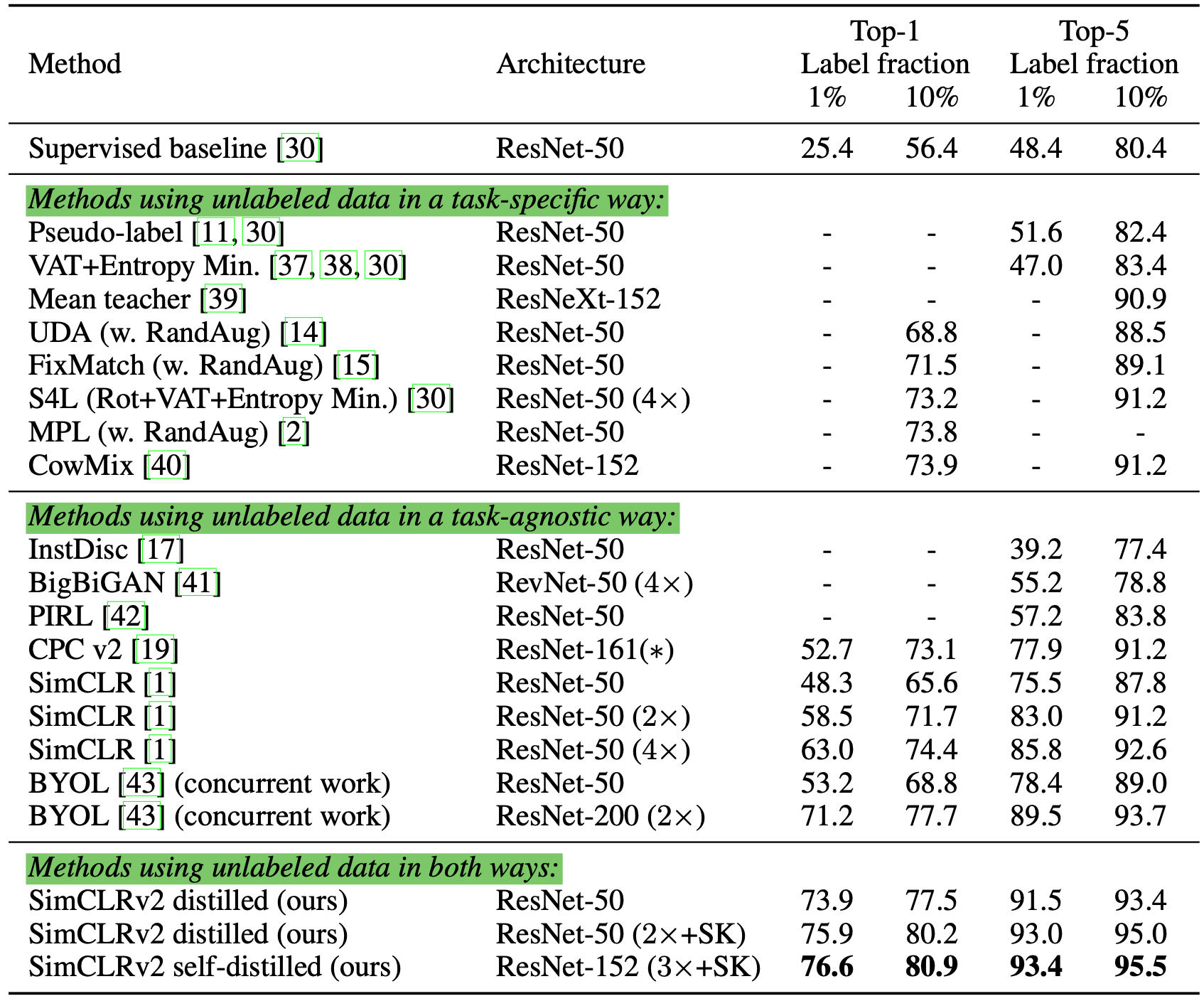
他们在ImageNet分类任务上进行了实验。自监督和预训练使用了SimCLRv2,这是一个SimCLR的直接改进版。他们的经验研究的一些发现与Zoph 等人, 2020的一致
- 更大的模型更加具有标签效率(label-efficient)
- SimCLR中使用大/深的映射头部可以改善数据表征学习
- 使用无标签数据进行蒸馏可以改善半监督学习
最近半监督学习中的常见主题总结,许多都是为了降低确认偏差的:
- 通过先进的数据增强方法来给样本添加有效的、多样的噪声
- 处理图片时,MixUp是一种非常有效的增强方法。Mixup也可以在语言任务中使用,可以带来很小的改进(Guo 等人, 2019)
- 设置阈值来释放低置信度的伪标签数据
- 每个mini-batch设置带标签样本数量的最小值
- 锐化伪标签分布来降低类别间的重叠度
引用
[1] Ouali, Hudelot & Tami.“An Overview of Deep Semi-Supervised Learning”arXiv preprint arXiv:2006.05278 (2020).
[2] Sajjadi, Javanmardi & Tasdizen“Regularization With Stochastic Transformations and Perturbations for Deep Semi-Supervised Learning.”arXiv preprint arXiv:1606.04586 (2016).
[3] Pham et al.“Meta Pseudo Labels.”CVPR 2021.
[4] Laine & Aila.“Temporal Ensembling for Semi-Supervised Learning”ICLR 2017.
[5] Tarvaninen & Valpola.“Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results.”NeuriPS 2017
[6] Xie et al.“Unsupervised Data Augmentation for Consistency Training.”NeuriPS 2020.
[7] Miyato et al.“Virtual Adversarial Training: A Regularization Method for Supervised and Semi-Supervised Learning.”IEEE transactions on pattern analysis and machine intelligence 41.8 (2018).
[8] Verma et al.“Interpolation consistency training for semi-supervised learning.”IJCAI 2019
[9] Lee.“Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks.”ICML 2013 Workshop: Challenges in Representation Learning.
[10] Iscen et al.“Label propagation for deep semi-supervised learning.”CVPR 2019.
[11] Xie et al.“Self-training with Noisy Student improves ImageNet classification”CVPR 2020.
[12] Jingfei Du et al.“Self-training Improves Pre-training for Natural Language Understanding.”2020
[13] Iscen et al.“Label propagation for deep semi-supervised learning.”CVPR 2019
[14] Arazo et al.“Pseudo-labeling and confirmation bias in deep semi-supervised learning.”IJCNN 2020.
[15] Berthelot et al.“MixMatch: A holistic approach to semi-supervised learning.”NeuriPS 2019
[16] Berthelot et al.“ReMixMatch: Semi-supervised learning with distribution alignment and augmentation anchoring.”ICLR 2020
[17] Sohn et al.“FixMatch: Simplifying semi-supervised learning with consistency and confidence.”CVPR 2020
[18] Junnan Li et al.“DivideMix: Learning with Noisy Labels as Semi-supervised Learning.”2020 [code]
[19] Zoph et al.“Rethinking pre-training and self-training.”2020.
[20] Chen et al.“Big Self-Supervised Models are Strong Semi-Supervised Learners”2020

更多推荐