这篇论文由Openai研究人员在2017年发布于arXiv上。论文改进了进化算法在强化学习中的应用，论文提出的方法极大地降低了不同进程间的通信量，让进化算法可以大规模并行。
背景及简介
随着深度学习的不断发展，当前对强化学习的研究绝大部分是基于深度学习的。在深度学习算法中，模型的优化依赖于优化器，常用的比如：Adam/SGD等。使用优化器对模型进行优化的一个问题是，它需要损失函数是可微的。面对一些不可微的情况，其中一种方法是使用重参数化等方法，将不可微的损失函数转化成可微的形式，再进行进一步计算。另外一类解决方案是使用进化算法这类黑盒优化算法。
进化策略（Evolution Strategies）在强化学习（RL）中的应用在很早以前就被人提出了，但是当前它并没有像深度学习一样如日中天。其中很大一部分原因是很多进化策略在模型参数量非常大的时候，会导致迭代速度非常慢。虽然有很多改进的方法，但是整体速度表现在很多情况下还是不能与基于深度学习的方法相比。
进化策略的一个优势是每一个个体/人口（population）可以并行。并行可以大幅改善算法优化的速度。当前，RL中非常流行的方法是策略梯度算法，一般，我们可以使用一个神经网络来拟合一个策略。策略梯度算法中，我们常用前面提到的优化器来对策略模型进行优化。这里显然我们也可以使用ES来对策略模型直接进行优化。为了充分利用ES可以并行的优点，我们希望可以进行大规模的并行（比如几千个CPU一起运算）。
然而，大规模并行方法在此应用时会带来通信带宽问题。即便是使用参数服务器，通行量也会随着服务器的数量线性增长。通信量的增长会带来很大的通信延时，进而导致并行的服务器CPU利用效率不高，而导致整体效率不高。本文对于此问题提出了一个非常简单实用的解决方案。
方法
进化策略
论文中使用的ES为自然进化策略（Natural Evolution Strategies, NES）算法，算法与我们之前介绍的一篇论文非常相似[2]。下面，我们介绍一下此进化策略。
在这个ES算法中，与使用优化器进行优化的算法一样，我们本质上还是希望找到一个可以让模型更优的一个方向。在深度学习中，我们通过计算损失函数的梯度得到方向向量，而在此ES算法中，我们直接使用服从某个分布的随机变量来测试出一个好的方向来。记我们的目标函数为$F(\theta)$，其中$\theta$为待优化的变量。我们的目标是最大化$F(\theta)$的期望：$\mathbb{E}_{\theta}F(\theta)$。在NES算法中，人口（population）使用参数为$\psi$的某个分布$p_\psi(\theta)$来表示，即目标函数转化为$\mathbb{E}_{\theta \sim p_\psi} F(\theta)$。假设我们可以使用梯度提升算法来求解，那么我们可以计算梯度：
$$
\begin{align*}
\nabla_{\psi} \mathbb{E}_{\theta \sim p_\psi} F(\theta) &= \nabla_\psi \int p_\psi(\theta)F(\theta) d \theta \\
&=\int F(\theta) \nabla_\psi p_\psi(\theta) d\theta\\
&=\int F(\theta) \cdot p_\psi(\theta) \nabla_\psi \log p_\psi(\theta) d \theta \\
&= \mathbb{E}_{\theta \sim p_\psi}\left[ F(\theta) \nabla_\psi \log p_\psi(\theta) \right] \tag{1}
\end{align*}
$$
我们假设$\theta$服从一个正态分布，那么我们可以将$\theta$表示成$\theta = \mu + \sigma \epsilon$，其中$\mu, \sigma$分别为正态分布的均值与标准差，$\epsilon$为服从标准正态分布的一个噪声变量。那么在给定均值与方差的情况下，$\theta$的变化完全由变量$\epsilon$决定，则有：
$$
\mathbb{E}_{\theta \sim p_\psi} F(\theta) = \mathbb{E}_{\epsilon \sim N(0, I)} F(\mu + \sigma \epsilon)
$$
其中变量$\psi = (\mu, \sigma)$，对$\psi$求导即对$\mu, \sigma$求导。我们先对均值$\mu$求梯度：
$$
\nabla_\mu \mathbb{E}_{\epsilon \sim N(0, I)} F(\mu + \sigma \epsilon) = \mathbb{E}_{\epsilon \sim N(0, I)}\left [ F(\mu + \sigma \epsilon) \nabla_\mu \log \phi_{\mu, \sigma}(\mu + \sigma \epsilon) \right] ; 使用公式(1)
$$
其中$\phi_{\mu, \sigma}$为均值为$\mu$标准差为$\sigma$的正态分布，我们将正态分布公式带入梯度求解有：
$$
\nabla_\mu \log \phi_{\mu,\sigma}(\mu + \sigma \epsilon) = \cfrac{\epsilon}{\sigma}
$$
故：
$$
\nabla_\mu \mathbb{E}_{\epsilon \sim N(0, I)} F(\mu + \sigma \epsilon) = \cfrac{1}{\sigma} \mathbb{E}_{\epsilon \sim N(0, I)} \left[ F(\mu + \sigma \epsilon) \epsilon \right]
$$
实际上论文中并未求解$\sigma$的梯度，在论文提出的算法中使用了固定的$\sigma$。文中并未指明使用的超参数$\sigma$是多少，实际使用时可以根据需要自行调节。
实际使用时，我们可以使用近似法求解$\mathbb{E}_{\epsilon \sim N(0, I)}$，即多次采样$\epsilon$然后求均值：
$$
\begin{align*}
\mathbb{E}_{\epsilon \sim N(0, I)} \left[ F(\mu + \sigma \epsilon) \epsilon \right] \approx \cfrac{1}{n} \sum_{i=1}^{n}\left[ F_i \cdot \epsilon_i \right] \ \ \tag{2}
\end{align*}
$$
算法
在公式$(2)$中，我们可以将对于不同的$\epsilon_i$取值的最终的奖励值$F_i$分给不同的进程/服务器去计算，以达到并行的目的。这里需要解决的是通信量的问题。论文中提供了一个非常巧妙的方案。
从公式$(2)$中，我们可以看出我们需要传递$F_i$与$\epsilon_i$的乘积。实际上$F_i$是一个标量，而$\epsilon_i$是一个（很长）的向量/矩阵，它的大小与我们模型的参数大小一致。由于$\epsilon_i$是一个服从正态分布的随机变量，那么我们可以使用伪随机的方式生成。使用伪随机方式的好处是一个序列仅由单个种子决定。这样我们得到一个序列仅需要传递一个种子即可。那么在实际通信时，仅需传递$F_i$与种子$seed_i$即可，极大地降低了通信量。算法的伪代码如下：
算法非常简洁，如果使用多进程而非多服务器的话，实现起来也非常简单。
实现细节参考
- 论文中在训练开始前生成了大量的高斯噪声（用于$\epsilon_i$），在迭代过程中，每个进程使用种子生成特定的下标序列来选择对应的高斯噪声。虽然这会导致变量之间不是完全的独立同分布的，但是实际效果还不错
- 实际使用时，如果并行度非常大，我们可以让每个子进程仅更新部分参数（甚至一个），这样算法中9~12行的计算量又减少了很多
- 可以对扰动量$\epsilon$使用镜像法，即同时计算扰动$\epsilon$与$-\epsilon$的奖励值
- 在参数更新前，对奖励值进行数量级的适配以让训练过程更加稳定
- 对参数采用weight decay以防参数相对于扰动值$\epsilon$来说变得过大
- 从算法中可以看出，每次运行都要完整运行完成一轮与环境的交互。而我们知道，与RL的环境交互时，有的策略运行步数长，有的则很短，这就有可能导致步数短的服务器CPU利用率不足。此时可以设置一个阈值$m$来限制最长运行步数。这个值可以动态调整（比如设置成所有进程平均步数的两倍）
- 在Atari环境中，此方法出现了探索不足的问题，文中指出使用virtual batch normalization可以解决此问题，此方法与batch normalization非常相似，感兴趣可参考相关论文
优点
- 无需计算梯度，在损失函数不可导情况下也可使用，并且无需担心long horizon问题
- 仅需知道最终的奖励总和，因此无需解决RL中的奖励如何分配给每个步骤的问题，也无需担心不同环境中每一秒帧数不一致的问题（比如Atari环境中通常会使用SkipFrame来让训练更稳定快速）
- 可以大规模并行。一小时的运行结果（使用了710个CPU并行）可以得到与A3C算法运行一天相匹配的性能
实验结果
在Atari 游戏中，有23个超过了A3C算法，28个不如A3C。
在MuJoCo任务中，为了达到与TRPO算法与环境交互5百万次的训练效果，ES算法需要与环境交互的步数与TRPO的比例如下表：
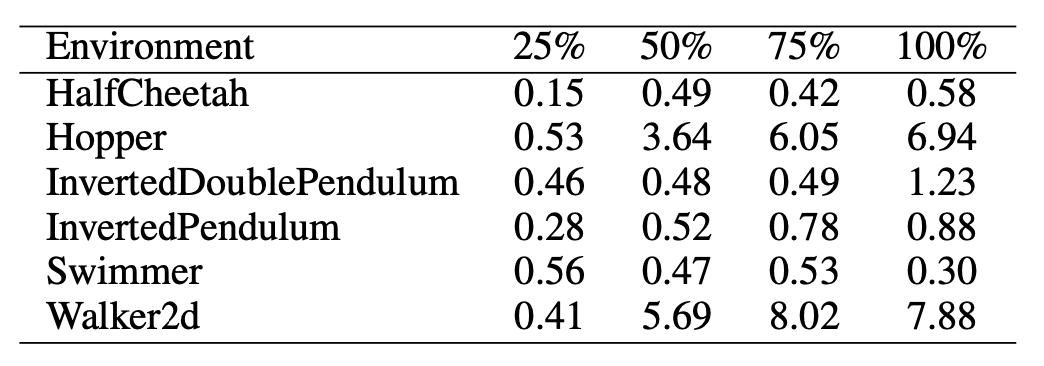
其中每一列表示分别达到TRPO训练25%/50%/75%/100% 步数的训练效果时，ES在不同环境上所需的步数比例。可以看到ES算法仅仅会在Hopper与Walker2d两个环境中需要明显多于TRPO的交互步数。但是考虑到如果可以大规模并行，ES实际的运行时间应该会大幅减小。
废话
这篇论文本来没打算分享的，但是我花了点时间实现了一下基本算法，并测试了一下HalfCheetah任务。我惊人地发现它实在太快了（^V^|||）。上上篇分享的CQL算法吧，训练这个任务，我调试了好长时间才勉强达到1000分，而且训练缓慢，基本训练要训个一天，还使用GPU（不知道是不是参数不对）。。。使用ES算法居然不到十分钟就可以达到2000+的水平，最好的效果还能上3000（电脑3950x，32核，用了31个并行进程）。看来在这种特征空间较小、信息量极大的任务上，进化算法还是有一定优势的。论文中的效果貌似应该是没怎么调参数的结果，最终性能不行，ES算法其实初始化、超参数啥的还是挺重要的，调好了训练应该挺快。
进化算法的话，在AI中感觉还是重视程度不够，个人认为十分有前途啊。
参考
[1] Salimans, Tim, et al. "Evolution strategies as a scalable alternative to reinforcement learning."arXiv preprint arXiv:1703.03864(2017).
更多推荐