这篇论文发表于今年的S&P，一作Jinyuan Jia目前在杜克大学攻读博士学位，他在安全顶会上已发表多篇文章，其所在实验室主要研究隐私与安全。本文的BadEncoder 提出了一种新的针对自监督学习（self-supervised learning）的后门攻击。
背景及简介
机器学习近年来得到了高速的发展，而随之而来的安全问题也越来越多地暴露出来。如今预训练模型大行其道，针对预训练模型的攻击也逐渐进入研究人员的视野。本文就是针对图片的预训练模型，提出了一种新的攻击方式BadEncoder。
文中使用对比学习算法SimCLR[2]来演示BadEncoder攻击算法。SimCLR发表于2020年的PMLR，是一个非常简洁的、用于提取视觉特征的对比学习算法。SimCLR包含三个主要组成部分：
- 数据增强：此部分使用各类图片增强算法用于生成图片的增强版
- 图片编码器：用于对图片进行特征提取
- 映射头部：用于将图片的特征向量映射到一个隐向量，此隐向量用于计算对比损失（contrastive loss）
在每一轮（batch）训练过程中，设有$N$个样本，那么SiMCLR使用增强算法生成$2N$个增强样本，属于同一图片的增强样本对被用作正样本对（positive pair），不同图片的增强样本被用作负样本对（negative pair）。算法的训练目标是增加正样本对之间的相似度，降低负样本对之间的相似度。相似度使用余弦相似度（consine similarity）来衡量。SimCLR的损失函数定义为所有正样本对的损失值之和，每个正样本对$(i, j)$的损失函数定义为：
$$
\mathcal{l} (i, j) = - \log \cfrac{\exp(sim(z_i, z_j)/\tau)}{\sum_{k=1, k\ne i}^{2N} \cdot \exp(sim(z_i, z_k)/\tau)}
$$
其中$z_i, z_j, z_k$为映射头部输出的隐向量，用于计算样本间的形似度（使用$sim$函数）；$\tau$为温度参数。这里需要注意一下$\mathcal{l}(i, j) \ne \mathcal{l}(j, i)$，所以（每一批次训练）最终的损失函数为$2N$项的均值，而不是$N$项。
BadEncoder
威胁模型
论文从攻击目标（goal）与攻击者的知识及能力两方面阐述了威胁模型。
攻击目标
攻击者希望在预训练模型中安插后门，从而可以让使用此预训练模型进行微调的下游任务中继承此后门，以达到攻击目的。我们假设攻击者去攻击$t$个下游任务，记第$i\ (=1, \ldots, t)$个下游任务为$T_i$，攻击者安插的后门记为$e_i$，攻击者期望安插此后门的样本被预测为标签$y_i$。攻击成功需要满足两个条件：
- 攻击的有效性：当下游任务$T_i$使用带后门攻击的预训练模型进行训练后，所有被安插后门$e_i$的测试样本都会被预测为标签$y_i$
- 攻击的可行性：安插后门的预训练模型不应该影响模型的正常使用，即没有后门的样本应该可以被正常预测为原本的标签
攻击者的背景及其能力
论文考虑两类攻击者：
- 预训练模型的原本训练者
- 对公开的预训练模型进行微调后的二次发布者
这两类攻击人员使用的安插后门的方式都是一样的，都是通过梯度下降算法来安插后门。
在BadEncoder攻击中，我们假设攻击者拥有一个影子数据集（shadow dataset）$\mathcal{D}_s$。两类攻击者的影子数据集类型可能是不一样的。对于第一类攻击者，即恶意的预训练模型提供商，他们的影子数据集就是他们用于预训练的数据集。对于二次训练的攻击者，他们有可能无法获取原始模型的预训练所用的数据集。那么他们所用的影子数据集的分布就可能与原始预训练数据集所用的是不一样的。
此外，攻击者需要有一个参考数据集（reference dataset）$\mathcal{R}_i = x_{i1}, \ldots, x_{ir_{i}}$（$r_i$为第$i$个攻击目标对应的参考集样本的数量）。该数据集对应了每一个攻击任务。对于一个攻击任务$(T_i, e_i, y_i)$，攻击者需要去搜集一个或多个标签为$y_i$的样本，用于安插后门之用。这一点很容易满足，随便在互联网上搜一搜即可得到。
攻击方式
我们上述的两个攻击目标，即有效性与可行性两方面来讨论攻击方式。首先为了达到有效性的目标，我们需要让带后门$e_i$的样本$x\oplus e_i$（$x$为干净样本）经过预训练模型输出的特征向量与对应标签$y_i$的样本所提取出的特征向量相似。记原始预训练特征提取编码器和带后门的编码器分别为$f$与$f^\prime$。那么$f^\prime(x)$与$f^\prime(x\oplus e_i)$之间的距离需要较小（文中使用余弦相似度来衡量两个向量之间的距离）。这样，我们可以直接使用梯度下降算法来对此距离进行训练优化。具体地，我们定义此项损失函数如下：
$$
L_0 = - \cfrac{\sum_{i=1}^t\sum_{j=1}^{r_i}\sum_{x\in\mathcal{D}_s}s(f^\prime(x\oplus e_i), f^\prime(x_{ij}))}{\vert\mathcal{D}_s \vert \cdot \sum_{i=1}^t r_i}
$$
其中$s$表示计算余弦相似度，$\vert \mathcal{D}_s \vert$为影子数据集的大小。
为了达成有效性的攻击目标，单单优化此距离还不够。原因是，$f^\prime(x)$经过优化之后，其所输出的特征向量很有可能远远偏离了原始的特征向量$f(x)$，那么使用$f^\prime(x)$进行下游任务训练后，下游任务预测出的标签就很有可能不是原始$x$所对应的标签$y$。因此，为了让我们的编码器不会在太大程度上改变原数据的编码，而仅仅学习了我们的后门，我们还需要尽量最小化$f^\prime(x)$与$f(x)$之间的距离。此项损失函数定义为：
$$
L_1 = -\cfrac{\sum_{i=1}^t \sum_{j=1}^{r_i} s(f^\prime(x_{ij}), f(x_{ij}))}{\sum_{i=1}^t r_i}
$$
为了满足可行性的要求，我们希望所有影子数据集中的数据经过后门编码器编码后的特征与原始编码器编码的特征之间的距离不大。距离损失函数定义为：
$$
L_2 = -\cfrac{1}{\vert \mathcal{D}_s \vert} \cdot \sum_{x\in \mathcal{D}_s}s(f^\prime(x), f(x))
$$
最终我们BadEncoder的优化问题为：
$$
\min_{f^\prime} L = L_0 + \lambda_1 \cdot L_1 + \lambda_2 \cdot L_2
$$
其中，$\lambda_1, \lambda_2$为超参数，用于控制三个损失函数之间的比重。
实际操作方法
论文实验中，实际操作方法为：首先训练原本的预训练编码器；而后，使用预训练编码器的参数权重来初始化后门编码器；后续，我们继续使用前面BadEncoder的损失函数$L$对后门编码器进行微调。最后，基于此后门编码器BadEncoder来训练下游的分类任务。
问题：这里直接将$L$加到原始预训练损失函数上一起进行训练能行吗？（而不是先训练预训练模型，而后再使用$L$进行微调。）
实验
文中使用了5个数据集：CIFAR10/STL10/GTSRB/SVHN/Food101。其中模型的预训练使用CIFAR10或者STL10。下游任务使用了除Food101之外的四个数据集。Food101仅用于研究影子数据集对BadEncoder的影响。
所使用的评价指标：
- 原始准确率（Clean Accuracy, CA）：不实用后门编码器及后门样本时，下游任务的准确率
- 后门准确率（Backdoor Accuracy, BA）：不带后门的原始样本在使用后门预训练编码器训练所得的分类器上所得的准确率。这个准确率主要是和CA进行对比，来看插入后门对预训练模型效果的影响
- 攻击成功率（Attack Success Rate, ASR）：测试带后门的样本$x\oplus e_i$，在使用后门预训练模型作为特征提取器训练得到的下游分类器上得到的准确率（检查是否等于$y_i$）。为了对比，实验还测试了$x\oplus e_i$在不带后门的下游分类器上被分类为$y_i$的比例作为基线，记为ASR-B
具体使用哪些分类作为目标以及超参数等细节，感兴趣可参考论文。
第一类攻击
攻击成功率
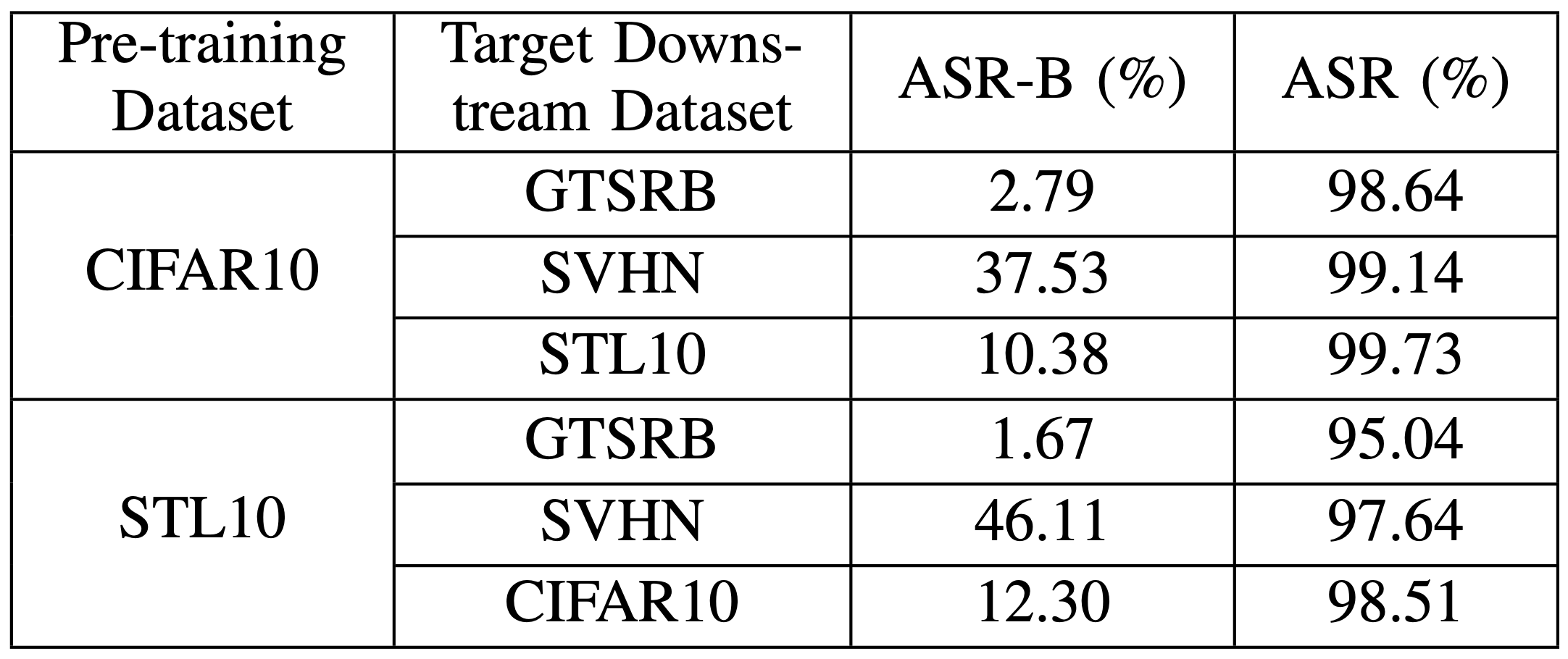
可以看到攻击成功率极高。
后门对原始任务准确率的影响
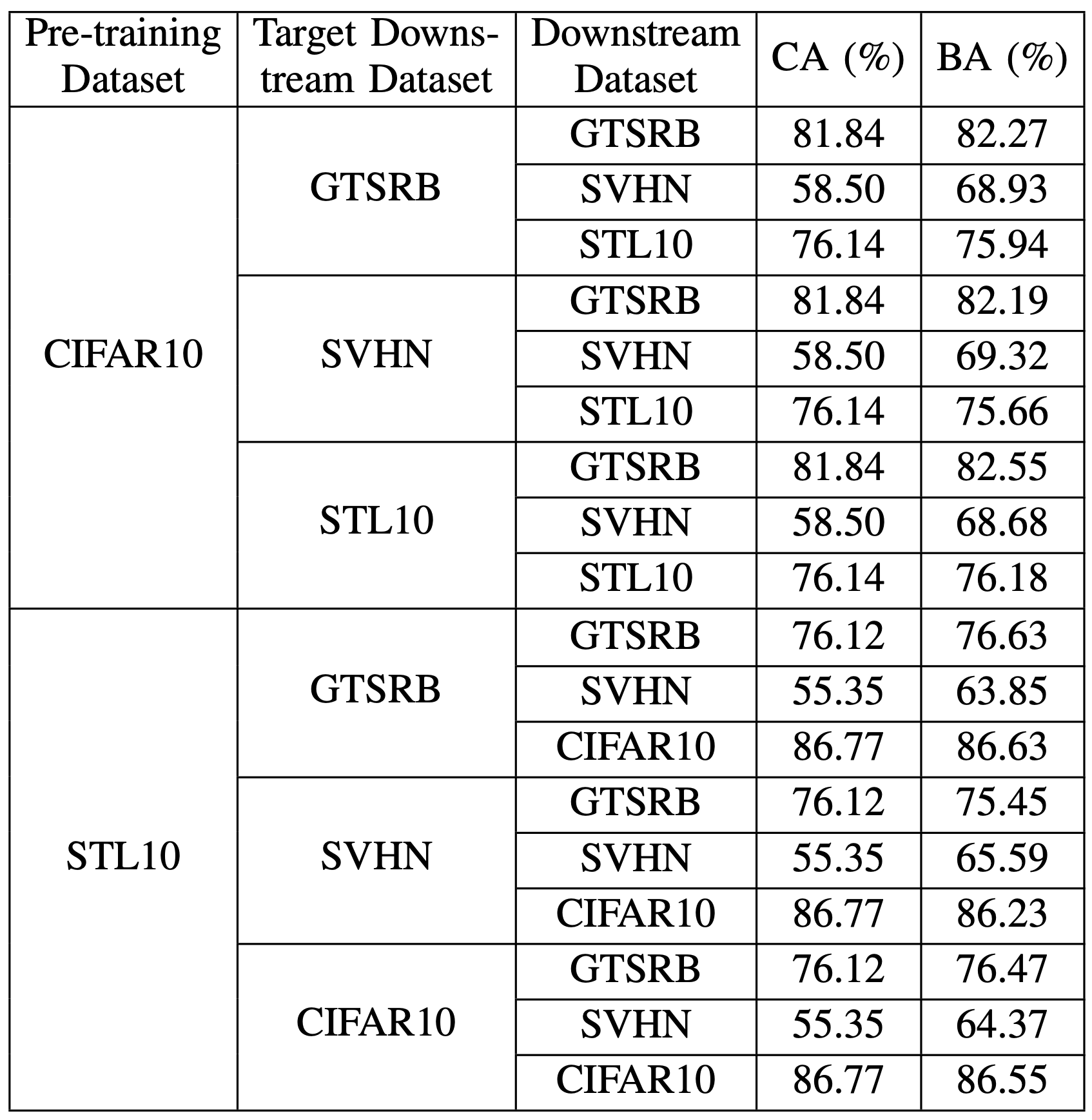
从上表可以看出，BadEncoder对准确率的影响在$1$%以内。而下游数据集为SVHN时，准确率居然还提高了。文中提出的解释是：SVHN数据集中包含很多噪声，而带后门的图片的加入后的微调让编码器可以生成更加鲁棒的特征。
二次微调攻击
文中选取了两个模型，一个是谷歌预训练的ImageNet，另外一个是CLIP模型。BadEncoder在这两个模型上的微调后，攻击成功率都极高并且对原始模型精度的影响都很小。对具体实验结果感兴趣可查看原论文。
攻击检测及防御
文中测试了两种现有的检测算法Neural Cleanse与MNTD，实际检测效果并不好。此外，论文还测试了一种可证明安全的防御机制PatchGuard，而实验表明，此种防御机制在实际中无法被应用（无法保证准确率）。PatchGuard 可以保证在后门$e_i$大小在满足某些特定的条件下（比如，我们的后门是在图片的右下角插入一个白方块，那么PatchGuard就会限制这个方块的大小），所预测出的标签受后门的影响也在一个特定范围内。但是，此方案的问题是，在后门大小固定的情况下，实际要达到防御目标，原任务的准确率几乎无法保证。比如，在本文的实验中，应用此防御机制后，BadEncoder 仍然可以达到50%左右的成功率，而此时，PatchGuard 可以的保证的准确率（certified accuracy）已经降为0。（这三个检测/防御机制我也没了解过，写的很可能不准确，感兴趣可查看原论文）。
参考文献
[1] Jia, Jinyuan, Yupei Liu, and Neil Zhenqiang Gong. "Badencoder: Backdoor attacks to pre-trained encoders in self-supervised learning."arXiv preprint arXiv:2108.00352(2021).
[2] Chen, Ting, et al. "A simple framework for contrastive learning of visual representations."International conference on machine learning. PMLR, 2020.
更多推荐