这篇论文发表在2021年的ICLR，一作Amy Zhang目前在加州伯克利做博士后，她同时还在脸书AI研究部门担任科学家。论文研究了在强化学习环境下在不使用数据重构（类似autoencoder）方法时，如何得到一个好的环境编码的问题。
背景及简介
在很多现实的应用中，如何从一个复杂多变的环境中学习到一个好的控制策略是非常关键的一步。深度强化学习在许多控制任务的模拟环境中，都取得了不错的成绩。但是现实环境的复杂度远比模拟环境要高得多。在实际环境中，一方面，数据采集的成本远远提高；另一方面，环境中的噪声元素太多。以自动驾驶为例，大多数模拟环境的背景都比较简单，但是现实生活中的驾驶环境中可能遇到的情况五花八门。一些算法在给定足够多的情况下，可以达到不错的性能表现，但是采样成本是实际应用无法绕过的一个门槛。因此，如何提高样本利用率（data efficiency）一直是强化学习中一个流行的研究问题。
既然在模拟环境中我们可以获取大量的数据，并训练得到一个模型，那么我们可否直接将模拟环境中得到的策略直接应用到实际环境中呢？显然，直接应用的话，模型的性能会大受影响。模拟环境中采样得到的数据与实际环境中采样得到的数据分布是不一致的。
本文提出的解决方案是，使用神经网络学习得到一个编码器，此编码器可以将状态数据编码到一个隐状态空间中，并且此编码器可以自动过滤掉环境数据中的噪声元素，只保留核心有用的部分。有了环境状态编码器之后，就可以得到一个低维度的环境向量。通过此低维度的隐环境向量，我们还可以高效训练一个环境的模型（不是神经网络模型，而是用于预测下一个动作（action）的输出状态（state）的模型）。这相当于我们得到了一个新的模拟环境，可以极大提高训练效率。
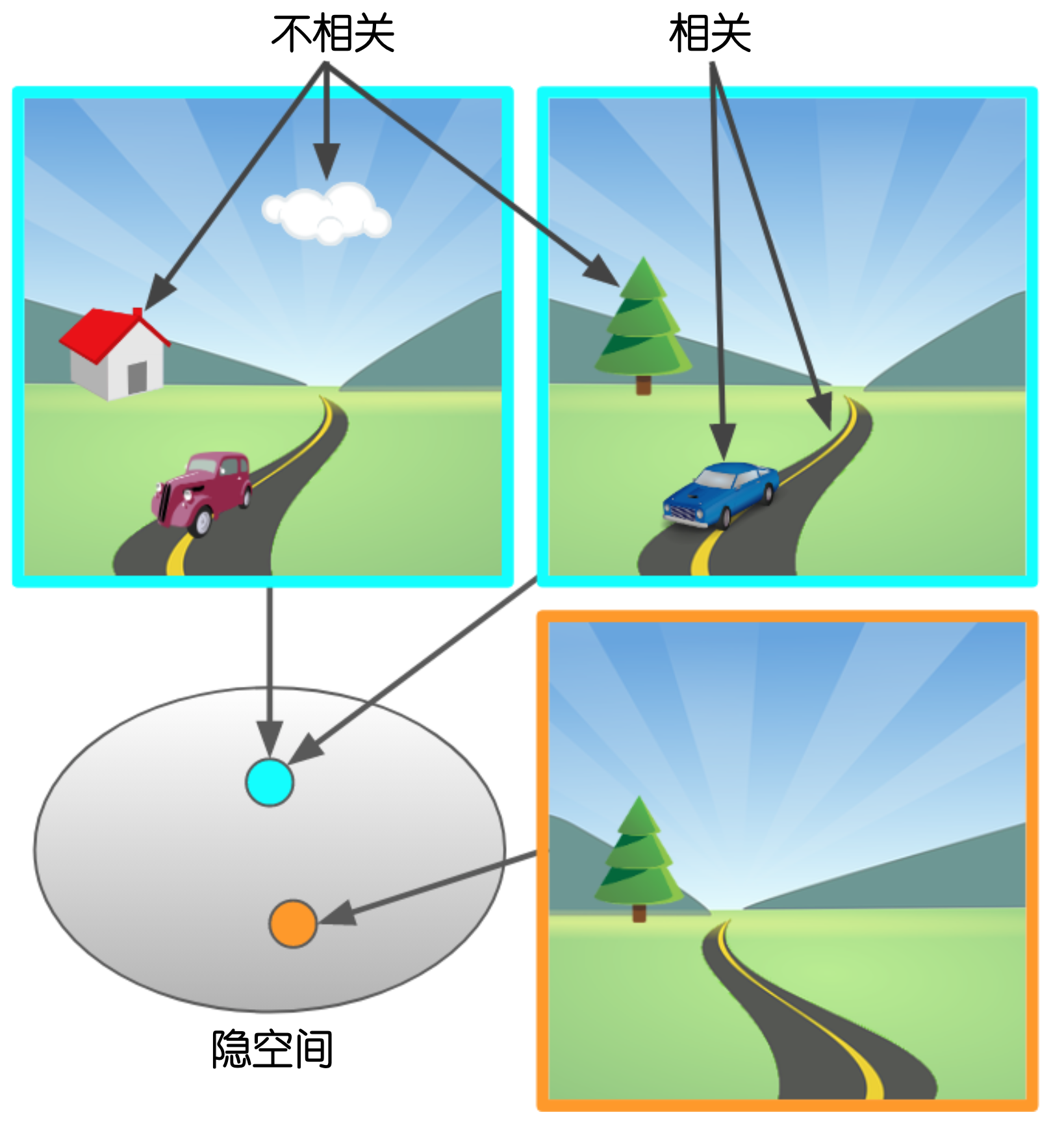
这里的核心问题是，如何才能学习到一个自动过滤背景噪声的编码器。显然，我们如果通过通用的自动编码器（autoencoder）训练得到的编码器不能满足要求。此编码器必须能够识别出有效的、与控制动作判定相关的数据。
算法（Deep Bisimulation for Control, DBC）
Bisimulation
本文提出的算法用到了一个比较重要的概念Bisimulation。此概念描述了一种状态之间的关系。如果两个状态是行为等效（behaviorally equivalent）的，那么我们称这两个状态之间为Bisimulation关系。形式化地，此关系需要满足以下两个条件：
$$
\begin{align*}
\mathcal{R} (s_i, a) &= \mathcal{R}\mathcal(s_j, a) & \forall a \in \mathcal{A} \tag{1}\\
\mathcal{P}(G\vert s_i, a) &= \mathcal{P}(G\vert s_j, a) & \forall a \in \mathcal{A}, \forall G \in \mathcal{S}_B \tag{2}
\end{align*}
$$
其中$s_i$表示状态（state）；$a$表示行为（action）；$\mathcal{R}$表示奖励（reward）；$\mathcal{P}$表示环境，一般我们可以理解为给定当前状态和动作的情况下，下一个状态的分布；$\mathcal{S}_B$表示某个等效状态划分的集合（集合的集合）。
从强化学习简单理解就是，等效状态中所有的状态，在执行任意动作后，得到的奖励是一样的，并且环境模型给出的下一状态也应该属于同一个等效状态划分。
这个概念太过抽象，我们在实际中无法直接应用，此概念提出$N$年之后，另外有人提出了一个称作Bisimulation 指标的东西，用于衡量两个状态之间的距离，以反映两个状态直接的等效程度：
$$
d(s_i, s_j) = \max_{a\in\mathcal{A}} (1-c)\cdot \vert \mathcal{R}_{s_i}^a - \mathcal{R}_{s_j}^a \vert + c \cdot W_1(\mathcal{P}_{s_i}^a, \mathcal{P}_{s_j}^a;d) \tag{3}
$$
其中$W_1$为一阶 Wasserstein 距离。
Bisimulation 指标直接反映了两个状态的行为等效程度。以图一为例，图一中三个驾驶背景（左上、右上、右下）应该是行为等效的。如果我们能够学习到一个编码器，它编码得到的状态可以直接反映Bisimulation 指标，那么此编码器的范化性应该会非常好。
DBC
我们使用$\phi$来表示编码器：$z_i = \phi(s_i)$。假设我们与环境交互得到两个样本：$(s_i, a_i, r_i, s_{i+1})$与$(s_j, a_j, r_j, s_{j+1})$，我们对上面的公式三稍作改变，得到论文中使用的指标：
$$
d^\prime = \vert r_i - r_j \vert + \gamma W_2(\hat{\mathcal{P}}(\cdot \vert \bar{\mathbf{z}}_i, a_i), \hat{\mathcal{P}}(\cdot \vert \bar{\mathbf{z}}_j, a_j))
$$
此公式中去除了$\max$操作，并且将Wasserstein距离从一阶换成了二阶。使用二阶Wasserstein距离$W_2$是因为，它在模型$\mathcal{P}$为高斯分布时，有一个非常好的解析式：
$$
\begin{align*}
& W_2(\mathcal{N}(\mu_i, \Sigma_i), \mathcal{N}(\mu_j, \Sigma_j))\\
=& \Vert \mu_i - \mu_j \Vert_2^2 + \Vert \Sigma_i^{1/2} - \Sigma_j^{1/2} \Vert_\mathcal{F}^2
\end{align*}
$$
其中，$\Vert \Vert_\mathcal{F}$为Frobenius范数/Euclidean范数，$\mathcal{N}$为高斯分布。此式简易证明参考[3]，详细参考[4]。
有了此指标之后，我们就可以训练编码器了。两个状态编码之间的距离$d_z = \Vert \mathbf{z}_i - \mathbf{z}_j \Vert_1$需要向$d^\prime$靠近。实际代码实现时，直接使用均方差损失即可。
由于$W_2$对于高斯分布有这么好的解析式，文中使用高斯分布对环境模型进行建模。
DBC算法流程为：对于第$t$步与环境的交互:
- 进行状态编码：$\mathbf{z}_t = \phi(s_t)$
- 对动作进行采样$a_t \sim \pi(\mathbf{z}_t)$，并执行$a_t$
- 将新样本存入缓冲区：$\mathcal{D} \leftarrow \mathcal{D} \cup \{ s_t, a_t, r_{t}, s_{t+1} \}$
- 从缓冲区中采样一批数据：$B_i \sim \mathcal{D}$
- 将$B_i$进行一次随机重排列得到$B_j$
- 使用其它强化学习算法进行策略的训练：$\mathbb{E}_{B_i}[J(\pi)]$
- 训练编码器：$\mathbb{E}_{B_i, B_j}[J(\phi)]$
- 训练环境模型：$J(\mathcal{P}, \phi) = (\hat{\mathcal{P}}(\phi(s_t), a_t) - \bar{\mathbf{z}}_{t+1})^2$
算法的训练过程包含三个部分：1. 原强化学习算法的训练；2. 编码器的训练；3. 环境模型的训练。
强化学习算法的训练
论文中将DBC与SAC（Soft Actor Critic）算法[6]相结合，对原SAC算法稍作变换，训练算法截图如下：
这里需要注意一点，就是使用了两个编码器（类似SAC中使用了两个Q函数）。第一行中我们看到$\hat{Q}$的计算时使用了目标编码器（target encoder）$\hat{\phi}$。最后一行对目标编码器进行了更新。
可以看到，训练SAC的过程中，反向传播可以自动协助训练编码器。
编码器的训练
编码器的训练目标是让得到的环境编码之间的距离与Bisimulation 指标尽可能靠近。直接使用均方差损失训练即可。
环境模型的训练
环境模型的训练目标是让模型给出的下一个状态的环境编码预测值$\hat{\mathbf{z}}_{t+1}$与实际的下一个状态编码$\mathbf{z}_{t+1}$尽可能接近。由于使用了高斯分布对环境模型进行建模，在实际实现时，我们的环境模型对应的神经网络模型$\mathcal{M}$输出的是下一个状态的均值$\mu$和方差$\Sigma$的预测。有了这两个变量后，我们就可以直接得到高斯分布的解析式$f_\theta = \mathcal{N}(\mu, \Sigma)$。
训练时，我们可以使用负对数损失函数（negative log）来训练：
$$
loss = - \sum_{t=1}^T \log \tilde{f_\theta}(\mathbf{z}_{t+1}\vert \mathbf{z}_t, a_t)
$$
将高斯分布的概率密度函数$f_\theta$带入负对数损失函数有：
$$
loss = \sum_{t=1}^T \cfrac{1}{2}\left( \cfrac{\mathbf{z}_t - \mu}{\Sigma} \right)^2 + \log \Sigma
$$
上式省略了训练无关的常数项。关于环境模型的训练，详细了解建议参考[5]。
关于具体实现，此论文作者开源了实验代码，可参考[2]。
理论分析
文中对DBC还进行了理论分析，感兴趣可参考原论文。
实验效果
文中进行了几组实验，这里我们展示下编码器的效果。下图展示了将得到的状态编码使用t-SNE可视化后的效果，其中左图为本文提出的算法，右图为其它算法。
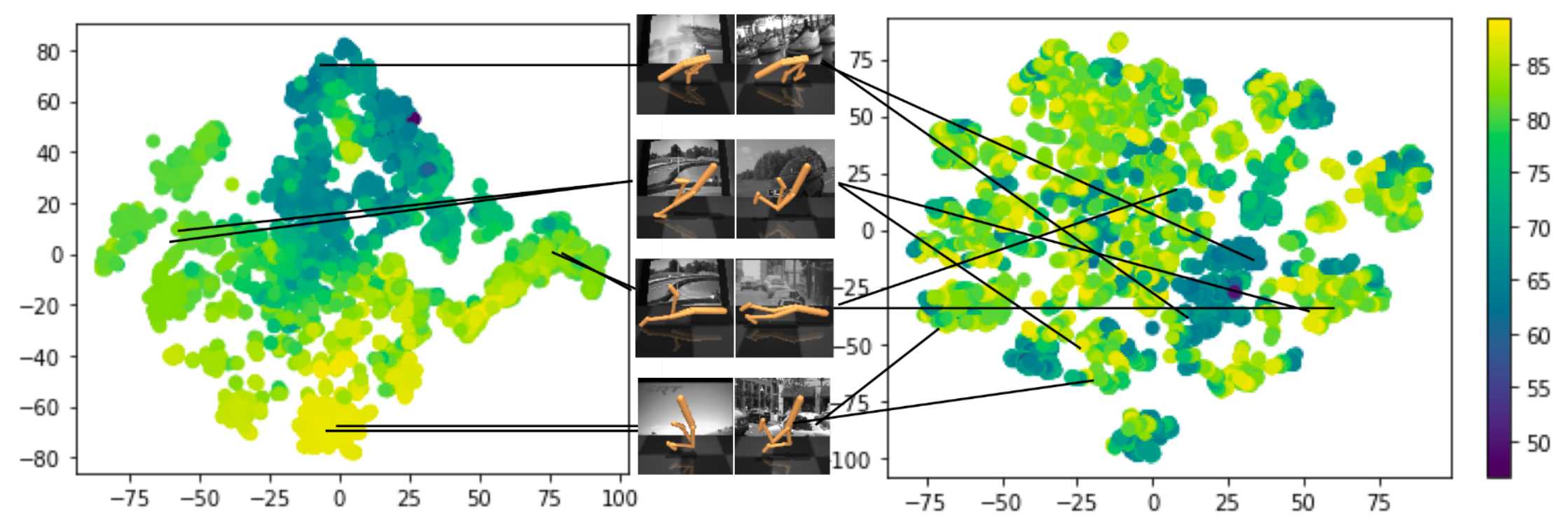
可以看出DBC对于背景不同的两张图片编码后，它们的距离非常接近；而右图中的VAE算法将不同背景的两张图片编码后，分布没有什么规律。
参考文献
[1] Zhang, Amy, et al. "Learning invariant representations for reinforcement learning without reconstruction."arXiv preprint arXiv:2006.10742(2020).
[2]https://github.com/facebookresearch/deep_bisim4control
[3] Wasserstein distance between two Gaussians,https://djalil.chafai.net/blog/2010/04/30/wasserstein-distance-between-two-gaussians/
[4] Givens, Clark R., and Rae Michael Shortt. "A class of Wasserstein metrics for probability distributions."Michigan Mathematical Journal31.2 (1984): 231-240.
[5] Chua, Kurtland, et al. "Deep reinforcement learning in a handful of trials using probabilistic dynamics models."Advances in neural information processing systems31 (2018).
[6] Haarnoja, Tuomas, et al. "Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor."International conference on machine learning. PMLR, 2018.
更多推荐