深度强化学习中的探索策略

本文翻译自：https://lilianweng.github.io/posts/2020-06-07-exploration-drl/，感谢Lilian Weng 的分享。

在强化学习中，探索与利用（exploration vs exploitation）是一个非常重要的主题。我们希望智能体（agent）可以尽可能快地找到最佳解决方案。而同时，在没有经过足够探索的情况所获取到的策略可能很糟糕。它很有可能是一个局部最优方案或者是一个失败的方案。以最大回报率为优化目标的现代强化学习算法可以非常高效地实施“利用”这一过程，但是，如何进行探索一直是一个开放讨论的话题。

这里，我想要讨论深度强化学习中的几个常用的探索策略。由于此话题太大，我的博客并没有希望覆盖所有重要的子课题。我计划定期更新这篇文章以逐渐丰富内容。

经典的探索策略

我们先来快速回顾一下在多臂机/表格式（tabular）强化学习问题上工作得非常好的几个经典探索算法。

• $\epsilon$-贪婪算法：智能体以概率$\epsilon$随机进行探索，以$1-\epsilon$概率采用最佳动作
• 上信心界算法（Upper confidence bounds）：智能体采用可以最大化上信心界$\hat{Q}_t(a) + \hat{U}_t(a)$的动作。其中$\hat{Q}_t(a)$为与时刻$t$前动作$a$相关的平均收益；$\hat{U}_t(a)$为与动作$a$被执行次数逆相关的函数（参考这里）
• 玻尔兹曼探索：智能体的动作服从玻尔兹曼分布（Q值经过softmax得到分布，使用了一个温度参数$\tau$）
• 汤普森采样：智能体维护一个最优动作的概率分布，从此分布中采样动作（参考这里）

在深度强化学习中，如果使用神经网络模型来进行函数拟合，那么下面的策略可以帮助进行更好地探索：

• 在损失函数中加入熵：鼓励智能体采用更加多样化的动作
• 基于噪声的探索：在观察到的状态（observation）、动作甚至参数空间中加入噪声来让动作多样化

探索中的核心问题

在环境（environment）很少提供奖励（reward）作为反馈或者环境中包含噪声的时候，想要得到一个好的探索策略是非常困难的。人们提出了很多的探索策略来解决我们下面提到的一些问题。

硬探索问题（Hard-Exploration）

所谓“硬探索”指的是在一个奖励极其稀疏或者飘渺的环境中探索困难的问题。在此类环境下，如果仅进行随机探索，那么几乎不可能成功，很难从环境中获取有意义的反馈。

经典的雅达利游戏Montezuma’s revenge就是硬探索问题的一个实例。很多论文都使用了此游戏来测试他们方法的有效性。

嘈杂电视问题

“嘈杂电视”问题始于论文Burda 等人, 2018中的一个思维实验。想象一下一个强化学习智能体，它会因为不断得到新的体验而获得奖励。那么，它在面对一个不可控的、会不断显示随机画面的电视（嘈杂电视）时，它会被电视上不断出现的画面所吸引。虽然电视上的这些画面可以不断地给智能体带来了新的体验（正反馈），但是智能体本身却没有学习到任何有价值的东西，它仅仅是成为了一个“电视迷”。

使用内在奖励作为探索红利

一个获取更好探索策略的方法（特别是解决硬探索问题）是对环境的奖励进行增强，即使用额外的奖励作为信号来激励更多的探索。此时，我们训练策略时所使用的奖励将由两部分组成：$r_t = r^e_t + \beta r^i_t$，其中$\beta$为平衡探索与利用的超参数。

• $r_t^e$为时刻$t$环境给出的外在奖励
• $r_t^i$为时刻$t$的内在探索红利

这里的内在奖励多多少少受到心理学中内在动机(intrinsic motivation)（Oudeyer & Kaplan, 2018）的影响。由新奇度驱动的探索可能是小宝宝成长和学习的一种重要方式。换句话说，探索活动应该是人类一种思想上内在的奖励，人类在潜意识里会去鼓励这种探索行为。内在奖励与好奇心、惊喜、熟悉度以及其它的一些因素相关。

同样的思想可以被应用到强化学习中去。在下面的小节中，我们将基于红利（bonus-based）的探索奖励大致分为以下两类：

1. 基于新状态的发现
2. 基于智能体关于环境认识的改善

基于计数的探索

如果我们将内在奖励视为一种惊喜，那么我们需要一种方式来衡量某个状态是少见还是经常出现。一种比较直观的衡量方式是记录下某个状态出现的次数，然后根据这个信息来定回报值。而后，利用此回报值我们可以引导智能体去探索那些被较少访问过的状态。这就是基于计数的探索方法。

令$N_n(s)$为记录状态$s$访问次数（从$s_1$到$s_n$）的经验函数。不幸的是，实现这样一个计数函数是不现实的，因为对于绝大多数状态$s$，$N_n(s)=0$，这个问题在连续以及高维状态空间中尤为突出。我们希望对于绝大多数状态，$N_n(s)$可以返回一个非零值（即使是之前尚未出现过的状态）。

使用密度模型

Bellemare 等, 2016使用了一个密度模型来近似状态的访问频率。他们同时设计了一个新的算法来从密度模型中推断出状态的访问次数。我们首先在状态空间上定义一个条件概率$\rho_n(s) = \rho(s \vert s_{1:n})$，它表示在给定状态$s_{1:n}$的情况下$s_{n+1}$出现的概率。对于此概率的估值，我们可以简单使用估计$N_n(s)/n$。

我们再来定义一个记录概率，作为访问完某个状态$s$之后密度模型更新的指导：$\rho'_n(s) = \rho(s \vert s_{1:n}s)$。

论文中引入了两个概念来规范密度模型的行为：一个伪计数函数$\hat{N}_n(s)$以及一个伪计数和（pseudo-count total）$\hat{n}$。由于密度模型被设计用来模拟计数，我们应该有：

$\rho_n(x)$与$\rho^\prime_n(x)$之间的这种关系要求密度模型必须是正向学习（learning-positive）的：对于任意状态$s_{1:n}\in \mathcal{S}^n$以及任意$s \in \mathcal{S}$，有$\rho_n(s) \leq \rho'_n(s)$。换句话说，在观察到一个状态$s$出现之后，密度模型对于同一状态的预测的概率应该是增加的。除了正向学习这个属性之外，密度模型必能能够以一种在线式、非随机的小批次样本的方式进行训练。这样自然而然地，我们可以有$\rho'_n = \rho_{n+1}$。

从上面给出的线性系统，我们可以计算出伪计数：

或者我们可以根据预测收益（prediction gain）来估计：

内在红利的一个常见的选择是使用$r^i_t = N(s_t, a_t)^{-1/2}$（类似MBIE-EB,Strehl & Littman, 2008）。基于伪计数的探索红利形式类似：$r^i_t = \big(\hat{N}_n(s_t, a_t) + 0.01 \big)^{-1/2}$。

Bellemare等,2016的实验中使用了一个简单的CTS（Context Tree Switching）密度模型来估计伪计数。CTS模型的输入为一张二维图片，输出一个基于位置的L型滤波器预测的乘积作为概率。其中每个滤波器的预测由在过去图片上进行训练的CTS算法给出。CTS算法非常简单，但是它在表达能力、可扩展性以及数据效率方面都有限制性。在之后论文中，Georg Ostrovski等,2017对此方法进行了改善，他们训练了一个PixelCNN（van den Oord 等,2016）模型作为密度模型。

正如在Zhao & Tresp，2018论文中展现的那样，密度模型也可以是高斯混合模型。在论文中，他们用了一个变分GMM来估计轨迹（连续的状态序列）的概率密度。此概率被用来在off-policy设定下作为经验回放（experience replay）的优先级。

哈希后计数

另外一种让对于高维状态进行计数成为可能的想法是将状态映射为一个哈希码。这样状态出现的次数就可以被跟踪计数（Tang等, 2017）。状态空间可以一个哈希函数$\phi: \mathcal{S} \mapsto \mathbb{Z}^k$进行离散化。此时，探索红利定义为$r^{i}(s) = {N(\phi(s))}^{-1/2}$，其中$N(\phi(s))$为$\phi(s)$的经验计数。

Tang等，2017中提出使用一个本地敏感哈希LSH（Locality-Sensitive Hashing）来将连续、高维的数据转化为一个离散的哈希码。LSH是一类基于特定相似度量的哈希函数。如果一个哈希方案$x \mapsto h(x)$可以保留数据之间的距离信息（也就是距离相近的向量之间它们对应的哈希代码之间也比较相似），那么我们称此哈希方案为本地敏感的（如果对此感兴趣可以看看LSH在Transformer改进中是如何应用的）。SimHash是一类计算高效的LSH，它使用角度距离来衡量相似度：

其中$A \in \mathbb{R}^{k \times D}$为一个从标准高斯采样得到的一个矩阵；$g: \mathcal{S} \mapsto \mathbb{R}^D$为一个可选的预处理函数。二进制码的维度为$k$，它用于控制状态空间的离散度。$k$越大，粒度越细，出现冲突的概率就越小。

对于高维度的图片，SimHash可能并不能在原始图片（像素点）上工作得很好。Tang等, 2017设计了一个自动编码器来学习状态$s$的哈希编码。它有一个由$k$个sigmoid函数组成的层输出中间隐状态，而后激活值$b(s)$被二值化（$\lfloor b(s)\rceil \in \{0, 1\}^D$）以作为状态$s$的哈希值。自编码器在$n$个状态的损失函数包含了两项：

这个方法存在一个问题，就是两个不相似的状态输入$s_i, s_j$可能会被映射到同样的哈希值上面，而此时自编码器却仍然可以完美地重建这两个（不相似）状态。你可以想象一下瓶颈层$b(s)$对应的哈希码为$\lfloor b(s)\rceil$，但是梯度是无法透过四舍五入函数进行反向传播的。我们可以通过使用注入均匀分布噪声的方式来部分缓解这个问题。注入噪声后，自编码器为了对抗这些噪声就需要将不同隐状态之间的距离拉得更大。

基于预测的探索

实现内在探索红利的第二种方法的思路是让智能体改善对环境的认识。智能体对环境中动态变化的熟悉程度可以通过一个预测模型来估计。使用预测模型来衡量好奇心的想法实际上在很久以前就被提出来了（Schmidhuber, 1991）。

前向动态（Forward Dynamics）

通过训练一个前向动态预测模型来反应模型对环境以及MDPs任务认知度是一种非常好的方法。前向动态预测模型可以捕捉智能体对于自己所执行动作导致的结果的预测能力：$f: (s_t, a_t) \mapsto s_{t+1}$。这种模型不可能是完美的（比如在部分可观察的环境中），因此误差$e(s_t, a_t) = | f(s_t, a_t) - s_{t+1} |^2_2$可以被用作内在探索奖励。预测误差越大，说明对于环境状态的越不熟悉。误差值掉得越快说明学习得越快。

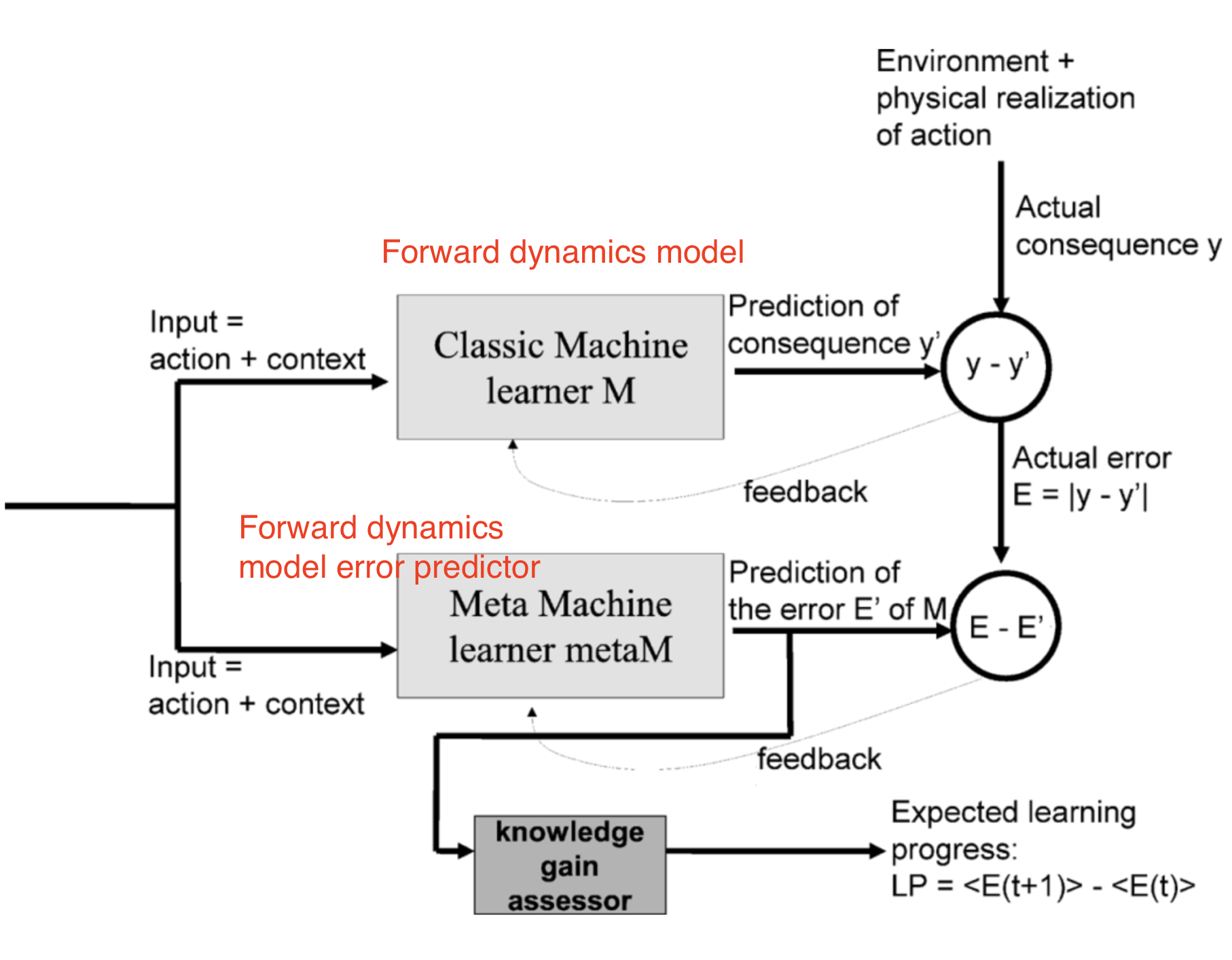
智能新奇度适配（Intelligent Adaptive Curiosity, IAC,Oudeyer 等, 2007）在使用前向动态模型来估计学习进程和指导内在探索奖励上，描绘了一个想法。

IAC依赖于一个记忆空间以及一个前向动态模型$f$。记忆空间用于存储机器人的所有经历$M=\{(s_t, a_t, s_{t+1})\}$。IAC根据状态转移逐步将状态空间（也就是机器人的感觉运动空间）分割成不同的区域。这个过程类似于决策树的构建：区域的分割发生在样本数量高于某一个阈值的时候，每一个叶子结点上，状态的多样性应该保持在一个最小值。每一个树节点都有其特色，并且有它自己的前向动态预测器$f$（称之为“专家”）。

专家的误差估计$e_t$被添加到一个与区域相关的列表尾部。学习进展的度量方式为偏移量为$\tau$的滑动窗口的平均错误率与当前滑动窗口值之差。内在奖励根据学习进展来定义：$r^i_t = \frac{1}{k}\sum_{i=0}^{k-1}(e_{t-i-\tau} - e_{t-i})$，其中$k$为滑动窗口的宽度。因此，预测错误率下降的越多，智能体就应该得到更大的内在奖励。换句话说，智能体被鼓励实行那些可以让其更快熟悉环境的动作。

Stadie等, 2015在一个由函数$f_\phi: (\phi(s_t), a_t) \mapsto \phi(s_{t+1})$定义的状态编码空间上训练了一个前向动态模型。模型在时刻$T$的预测误差被进行了归一化（使用截止时间$t$的所有误差的最大值进行归一化$\bar{e}_t = \frac{e_t}{\max_{i \leq t} e_i}$）。内在奖励基于此来定义：$r^i_t = (\frac{\bar{e}_t(s_t, a_t)}{t \cdot C})$，其中$C\gt 0$为衰减常量。

使用$\phi(\cdot)$来对状态进行编码是必要的，论文实验表明在原始像素点数据上进行动态模型的训练会导致非常不给力的表现（对所有状态都给出同样的探索红利）。在Stadie等, 2015中，编码函数$\phi$是通过一个自动编码器学习而来的，$\phi(\cdot)$就是自动编码器中某一层的输出。自动编码器的训练样本可以使用一个随机智能体自动搜集而来，也可以随着策略（训练前期可以使用$\epsilon$探索）的更新一起迭代训练。

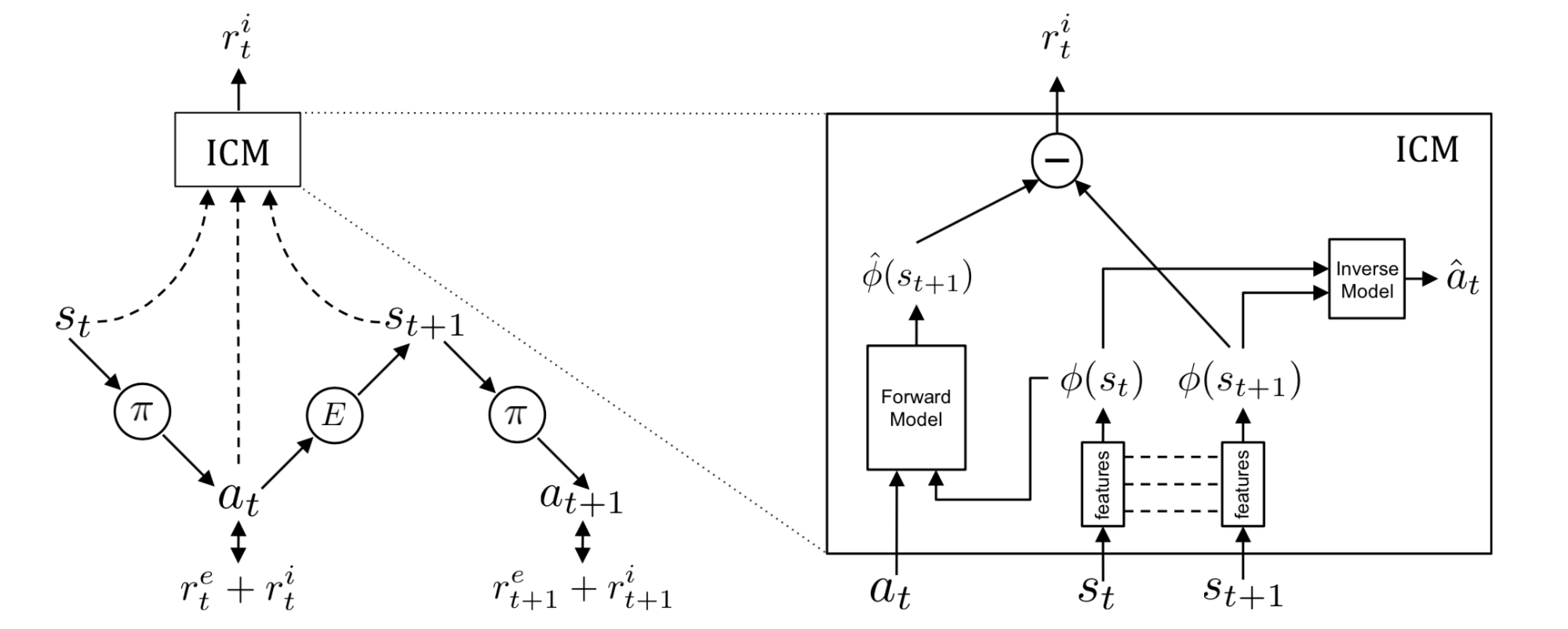
内在新奇度模块（Intrinsic Curiosity Module, ICM,Pathak 等, 2017）中没有使用自动编码器，而使用了一个自监督逆向动态模型来学习状态空间编码器$\phi(\cdot)$。给定一个智能体动作的情况下去估计下一个状态这件事并没有那么容易，特别是考虑到环境中的一些因素是无法被智能体所控制的或者环境中的一些因素对于智能体是不会产生影响的。ICM相信一个好的状态特征空间应该可以排除一些对智能体不会产生影响的因素，智能体也不会有动力学习这些无关的环境因素。通过学习一个逆向动态模型$g: (\phi(s_t), \phi(s_{t+1})) \mapsto a_t$，特征空间中仅会抓住那些与智能体动作相关的因素，而忽略其余的。

给定一个前向模型$f$，一个逆向动态模型$g$以及一个观察$(s_t, a_t, s_{t+1})$：

这样，所得到的$\phi(\cdot)$期望可以对于环境中的一些不可控因素展现出鲁棒性。

Burda, Edwards & Pathak 等, 2018对于纯新奇驱动（curiosity-driven）的学习进行了大范围的比较实验（纯新奇驱动表示仅内在奖励被提供给智能体）。在这篇研究中，奖励为$r_t = r^i_t = | f(s_t, a_t) - \phi(s_{t+1})|_2^2$。特征编码器$\phi$的选择对于学习前向动态至关重要，它应该是紧凑的、高效的以及稳定的。这样就可以让预测任务更加易于处理，并且可以过滤掉不相关的因素。

对比如下四个编码函数：

1. 原始图片像素：不编码，即$\phi(x) = x$
2. 随机特征（Random Features, RF）：每个状态通过一个固定的随机神经网络来压缩
3. VAE：概率编码器被用于编码，$\phi(x) = q(z \vert x)$
4. 逆向动态特征（Inverse dynamic features, IDF）：与ICM同样的特征空间

实验中所有的奖励都使用了累计回报标准差的估计进行了归一化。所有实验都在一个无限范围的环境（infinite horizon setting）中进行，以防止“结束”标志泄漏了信息。

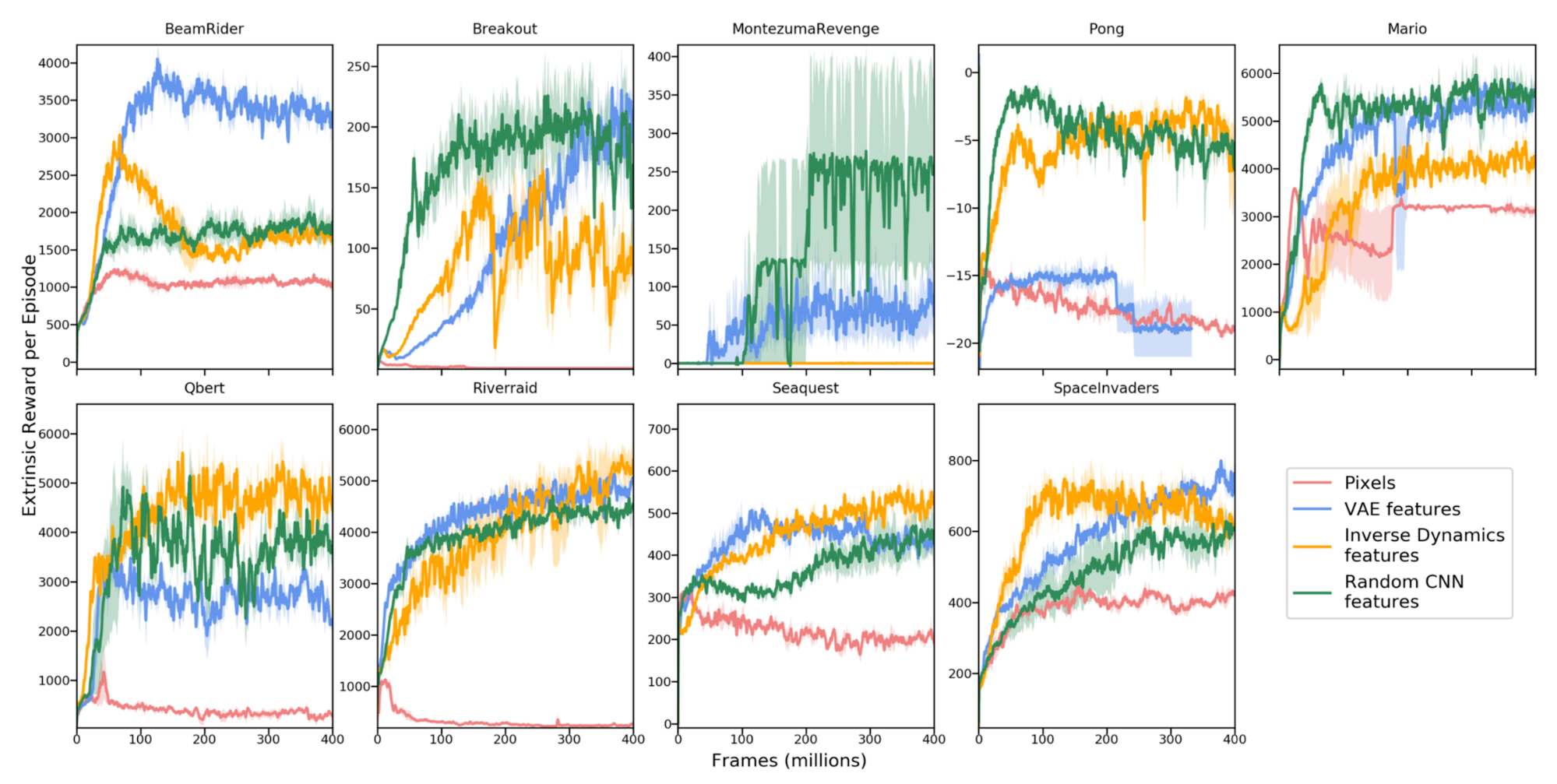
有意思的是随机特征竟然表现得很有竞争力。但在特征迁移实验中（也就是：使用超级玛丽1-1训练的智能体在其它关卡中进行测试），IDF特征的范化性更好。

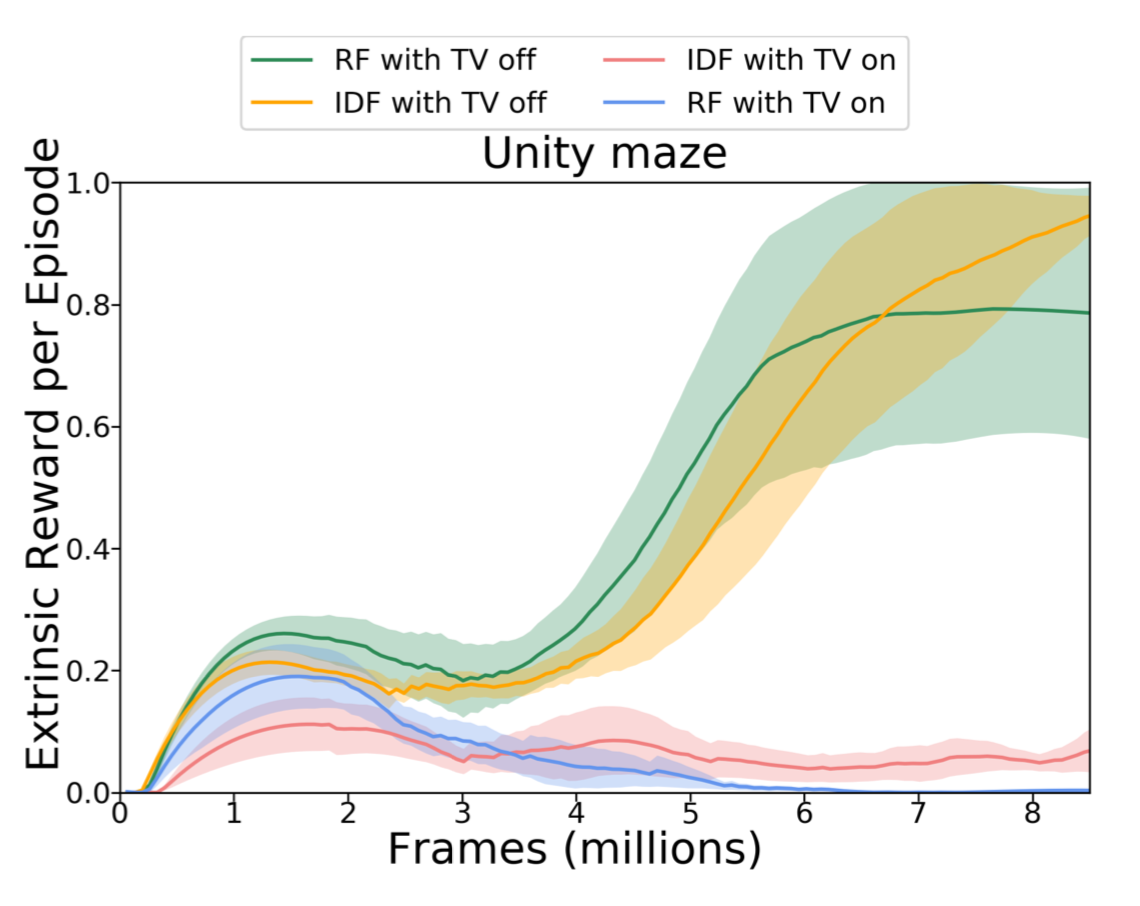
他们还在一个存在嘈杂电视的环境中比较了RF与IDF。不出意外，噪声电视极大地减缓了学习过程，并且即时的外部奖励少了很多。

前向动态优化也可以通过变分推断来进行建模。VIME（Variational information maximizing exploration,Houthooft 等, 2017）是一种基于环境动态信息收益（information gain）最大化的探索策略。获取多少额外的前向动态信息可以通过熵的减少来衡量。

令$\mathcal{P}$为环境状态转移函数，$p(s_{t+1}\vert s_t, a_t; \theta)$为前向预测模型（$\theta$为参数），$\xi_t = \{s_1, a_1, \dots, s_t\}$为历史轨迹。我们希望在实行某一动作并观察到下一个状态后可以降低熵，也就是最大化如下值：

我们希望在取期望（所有可能的下一个状态）的情况下，智能体所采取的动作可以提高新旧模型参数分布间的KL散度（信息收益）。这一项可以作为内在奖励被添加到奖励函数中去：$r^i_t = D_\text{KL} [p(\theta \vert \xi_t, a_t, s_{t+1}) | p(\theta \vert \xi_t))]$。

但是，计算后验分布是不可行的。

由于很难直接计算$p(\theta\vert\xi_t)$，一个很自然的选择就是使用一个分布$q_\phi(\theta)$来近似。使用变分下界，我们知道$q_\phi(\theta)$的最大化就等价于最大化$p(\xi_t\vert\theta)$以及最小化$D_\text{KL}[q_\phi(\theta) | p(\theta)]$。

使用近似分布$q$，内在奖励变为：

其中$\phi_{t+1}$表示$q$的参数。使用KL散度的中位数进行归一化之后，它被用作探索红利。

这里动态模型被参数化为贝叶斯神经网络，它维护了权重的分布。BNN的权重分布$q_\phi (\theta)$被建模为一个全分解高斯，参数$\phi = \{\mu, \sigma\}$。我们很容易采样得到$\theta \sim q_\phi(\cdot)$。使用二阶泰勒展开后，KL项$D_\text{KL}[q_{\phi + \lambda \Delta\phi}(\theta) | q_{\phi}(\theta)]$可以使用Fisher信息矩阵$\mathbf{F}_\phi$（很容易计算）进行估计。由于$q_\phi$为可分解高斯，因此，协方差矩阵是一个对角阵。查看论文以获取更多细节，特别是其中的章节2.3-2.5。

所有上述方法都是依赖于单个预测模型的。如果我们有很多个这样的模型，我们可以使用模型间的不一致性来作为探索红利（Pathak 等, 2019）。高度的不一致性意味着对于预测的信心不足，因而需要更多的探索。Pathak等,2019中提出训练一系列的动态模型，并使用模型输出集合的方差来作为探索红利$r_t^i$。更精确地来说，他们将状态空间编码为随机特征，并且学习了5个模型。

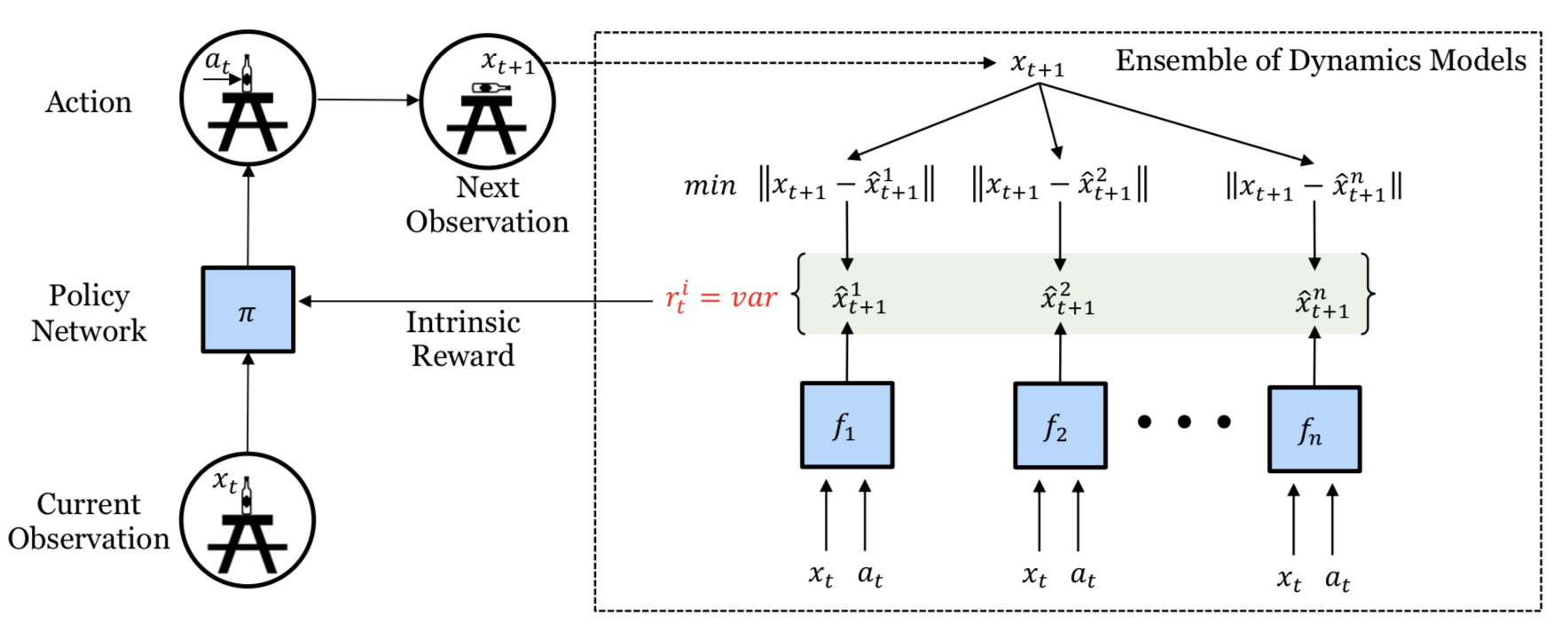
由于$r_t^i$是可微的，模型的内在奖励可以直接通过梯度下降来进行优化，从而改变智能体的动作。这种可微性非常高效，但是受限于非常短的探索步骤。

随机网络

但是，如果预测任务与环境中的动态变化一点关系没有怎么办呢？结果表明即使是一个随机任务，预测对于探索仍然是有帮助的。

DORA（Directed Outreaching Reinforcement Action-Selection;Fox & Choshen 等, 2018）是一个新的框架。它基于一个新引入的、任务不相关的MDP来注入探索信号。DORA的思想依赖于两个并行的MDPs：

• 一个是原始任务MDP
• 另外一个是同样的MDP但是不带奖励（no reward attached）：每一个状态-动作对被设计为具有值0。从这第二个MDP学习到的Q值被称为E值。如果模型不能完美将E值预测为0，那么它仍然缺失信息

初始E值被设置为1。这样的正值初始化可以鼓励正向探索以更好地预测E值。高E值的状态动作对说明没有搜集到足够多的信息，至少不足以排除高E值。从某种程度上看，E值的对数可以被看作是对访问计数的一种泛化。

当使用神经网络来拟合E值函数时，会在神经网络上额外添加一个头部（它被简单用于预测E值）。给定E值$E(s_t, a_t)$，探索红利为：$r^i_t = \frac{1}{\sqrt{-\log E(s_t, a_t)}}$。

与CORA类似，随机网络蒸馏（Random Network Distillation, RND;Burda 等, 2018）方法中引入了一个独立于主任务的预测任务。RND的探索红利被定义为一个神经网络$\hat{f}(s_t)$的预测误差。该神经网络用于预测一个固定随机初始化的神经网络对环境观察（observations）的特征编码。这里的动机是：给定一个新的状态，如果相似的状态在过去被访问过许多次，那么预测就会变得很容易，误差就小。探索红利定义为$r^i(s_t) = |\hat{f}(s_t; \theta) - f(s_t) |_2^2$。

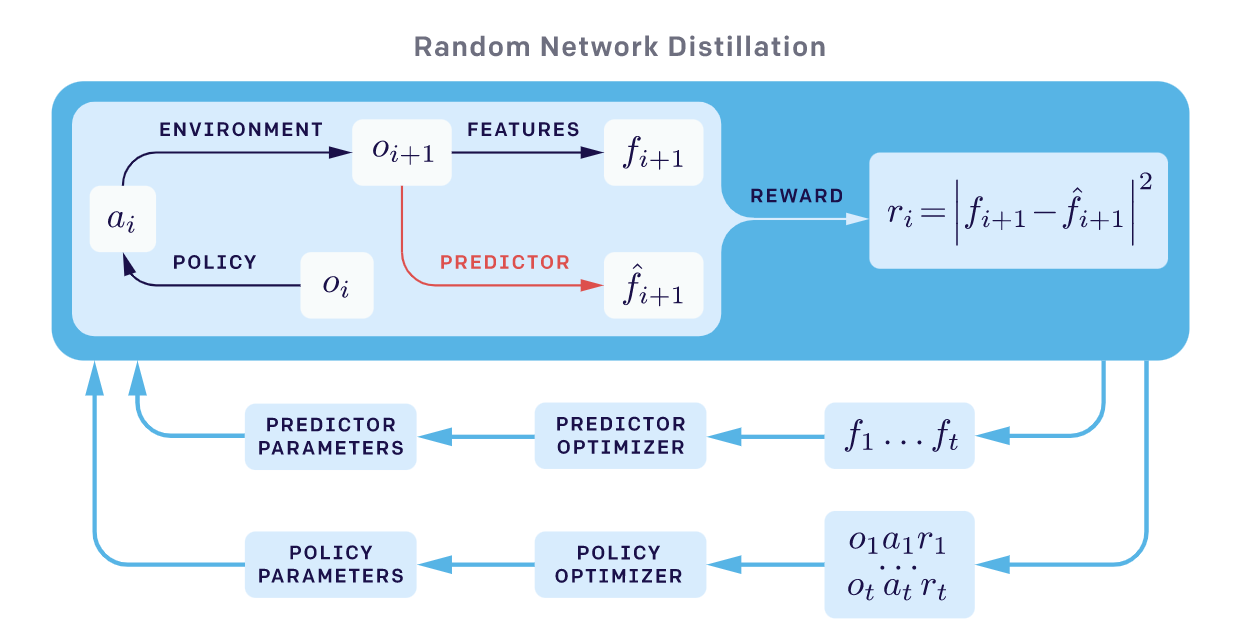
RND实验中有两点很重要：

1. 非阶段性设置（non-episodic setting）可以带来更好的探索，特别是在不使用任何外部奖励的时候。这意味着回报不会在“游戏结束”时被截断，而内在回报可以在多个并行的进程中传播
2. 归一化很重要，因为在给定一个随机网络的输出作为目标时，奖励的数量级很难调整。内在奖励的归一化是通过除以一个估计（使用内在回报的标准差）实现的

RND可以很好地解决硬探索问题。举例来说：在Montezuma's Revenge游戏中，使用最大化RND探索红利的方式智能体始终可以找到超过一半的房间。

物理性质

不同于模拟器里的游戏，一些现实的强化学习应用（比如机器人）需要对物理世界中的对象以及直观推理有一定的了解。一些预测任务还需要智能体与环境间进行一些列连续的交互，并且观察相应的结果（比如预测一些类似密度、摩擦力等等的物理隐藏属性）。

基于此想法，Denil等, 2017发现深度强化学习智能体可以通过学习来进行必要的探索以发现隐藏属性。准确说来，他们考虑了两个实验：

1. "哪一个更重？"：智能体必须与物理块进行交互来推断哪一个更重
2. “塔”：智能体需要通过将塔推到来推断塔由多少个实体组成

首先，实验中的智能体通过一个探索阶段与环境进行交互以便搜集信息。一旦探索阶段结束了，智能体被要求输出一个打标签的动作来回答问题。如果答对了，智能体会得到一个正奖励，否则得到一个负奖励。正确答案需要智能体与环境中的物体进行大量的交互、有效的玩耍。在此过程中，探索自然而然地就发生了。

在他们的实验中，智能体可以在这两个任务中学习。智能体的性能表现会随着任务的难度而变化。论文中没有使用物理预测任务来提供内在红利奖励，也没有使用与其它学习任务相关的外部奖励，而是专注于探索任务本身。我确实非常喜欢通过预测环境中隐藏的物理属性来进行复杂探索的想法。

基于记忆的探索

基于奖励的探索有几个缺点：

• 函数拟合跟不上
• 探索红利为非平稳的
• 知识衰退：这意味着状态不再具备新奇度，因此不再能够及时提供内在奖励信号

本节中的方法依赖于外部记忆来解决基于奖励的探索。

阶段记忆

正如上面提到的一样，RND在非分段式（non-episodic）设置下可以工作的更好，这表明预测的知识是在多阶段（episodes）上累积的。NGU（Never Give Up;Badia 等, 2020a）探索策略将两个新奇模块（novelty module）组合起来：一个可以快速适配阶段（episode）内环境的模块；一个使用RND可以作为一个终身学习的模块。

准确来说，NGU中的内在奖励由两个模块中的两部分探索红利组成，分别为阶段内探索红利与多阶段探索红利。

短期的阶段内奖励由一个阶段新奇度模块提供。此模块包含了一个阶段记忆$M$（动态大小、插槽式）与一个IDF嵌入函数$\phi$（与ICM中的特征编码一样）。

1. 在每一步中，当前状态嵌入表示$\phi(s_t)$被添加到记忆$M$里
2. 内在红利通过比较当前的观察与记忆$M$中的内容相似度来决定。更大的差异意味着更大的红利

其中$K(x, y)$是衡量两个样本间距离的核函数。$N_k$为$M$中$k$个最近的邻居（根据核函数$K(\cdot, \cdot)$）的集合；$c$是一个很小的常数用于防止分母为0。在论文中，$K(x, y)$被配置为逆核（inverse kernel）：

其中$d(\cdot,\cdot)$为两个样本间的欧几里得距离；为了更好的鲁棒性，$d_m$为$k$个最近距离样本间欧几里得距离平方的滑动平均。

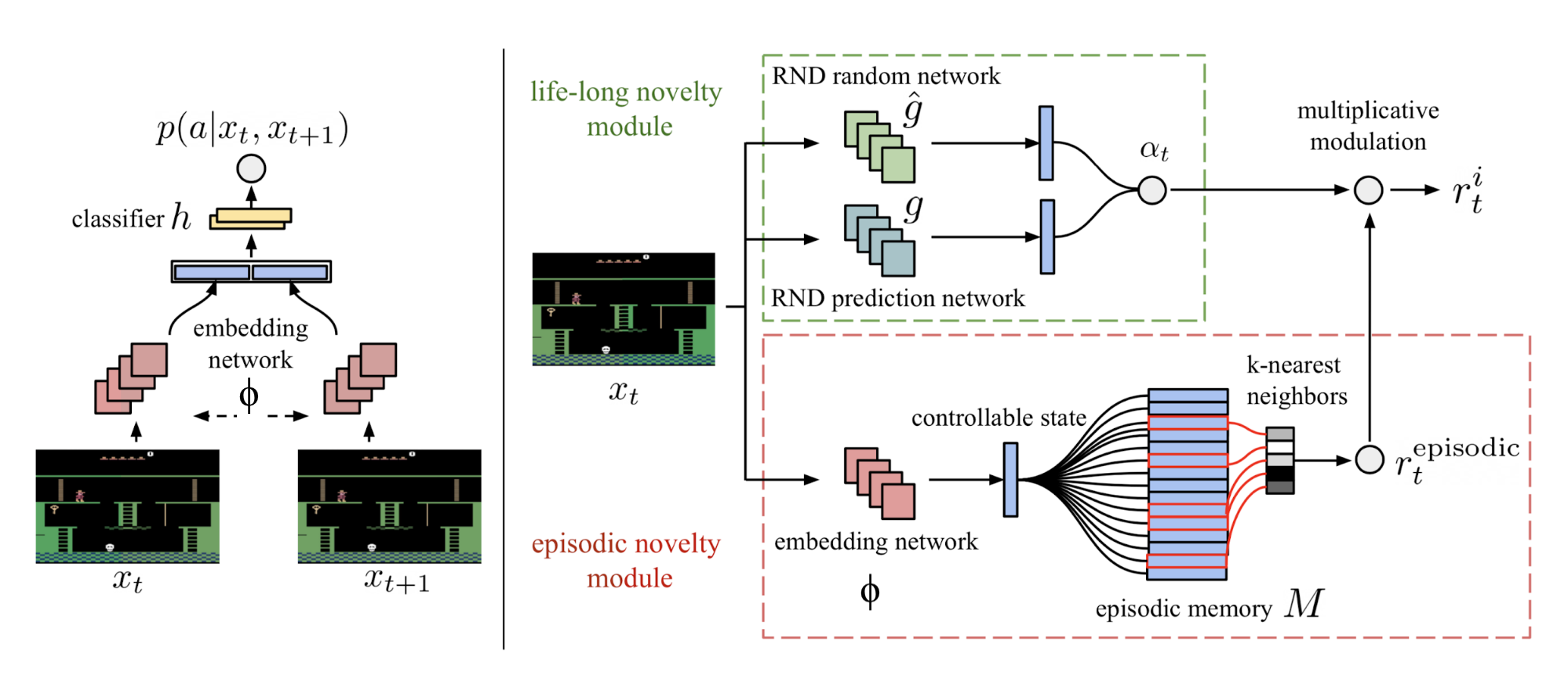
长期的跨阶段的新奇度依赖于RND在长期新奇模块中给出的预测误差。探索红利是$\alpha_t = 1 + \frac{e^\text{RND}(s_t) - \mu_e}{\sigma_e}$，其中$\mu_e, \sigma_e$为RND误差$e^\text{RND}(s_t)$的均值与标准差的滑动平均值。

但是在RND 论文的结论小节，我发现了如下表述：

“我们发现，RND探索红利对于局部探索是足够的，即对可以由短期决策即可决定结果的探索够用（比如是否需要与某个对象进行交互或者回避）。而涉及长期协调决策的全局探索则已超过了我们方法的能力范围。”

这里我有一点疑问，RND是如何被用做一个很好的终身新奇度红利提供者的。如果你知道为什么，请在下方自由评论。

最终组合的内在奖励为$r^i_t = r^\text{episodic}_t \cdot \text{clip}(\alpha_t, 1, L)$，其中$L$为最大奖励常数，$\text{clip}$为截断函数。

NGU的设计让它拥有了两个非常漂亮的性质：

1. 在同一阶段内，快速降低对于同一状态的兴趣
2. 缓慢降低对在不同阶段出现过多次的状态的兴趣

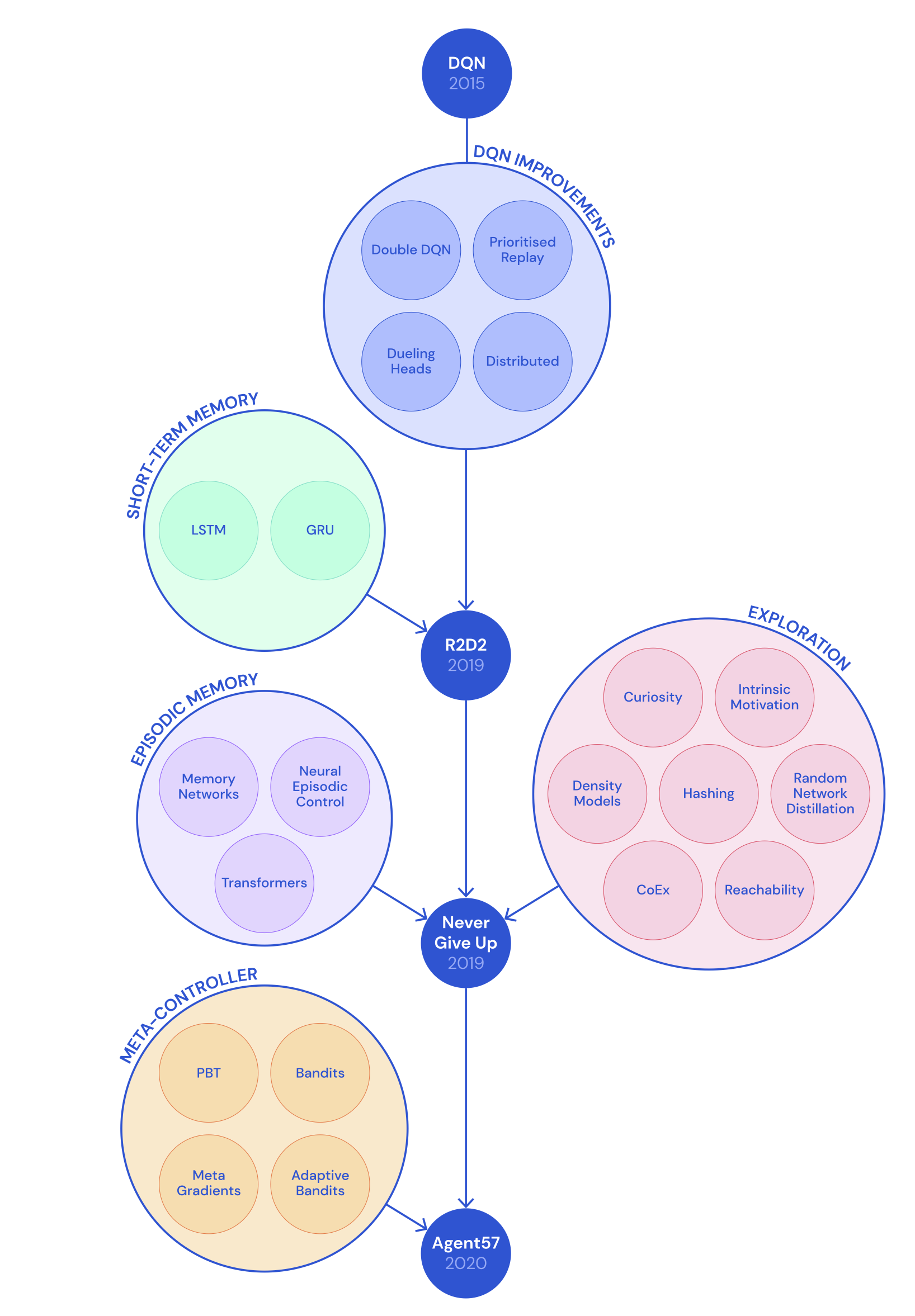
后来，在NGU之上，DeepMind提出了"Agent57"（Badia等, 2020b），这是首个可以在所有57个雅达利游戏上可以超越人类基准的深度强化学习智能体。Agent57在NGU之上的两个主要改进点为：

1. Agent57中使用不同的探索参数对$\{(\beta_j, \gamma_j)\}_{j=1}^N$训练了多个策略。回顾一下，给定$\beta_j$，奖励的构成为$r_{j,t} = r_t^e + \beta_j r^i_t$，$\gamma_j$为奖励衰减系数，$r^e, r^i$分别对应外部奖励和内在奖励。很自然地我们可以认为：更大的$\beta_j$以及更小的$\gamma_j$可以在训练早期取得更多的进展；而随着训练的进行，参数应该往相反方向调整。一个元控制器（基于滑动窗口的UCB多臂机算法）被训练用来选择哪一个策略的优先级较高
2. 第二个改进是一个新的Q值函数参数化方法。它将内在与外在奖励的贡献进行了分解组合为一个绑定的收益：$Q(s, a; \theta_j) = Q(s, a; \theta_j^e) + \beta_j Q(s, a; \theta_j^i)$在训练期间，$Q(s, a; \theta_j^e)$与$Q(s, a; \theta_j^i)$分别使用了奖励$r_j^e$与$r_j^i$进行优化

在阶段性记忆（episodic memory）中的状态之间距离的衡量方面，Savinov等, 2019没有使用欧几里得距离，转而考虑状态之间的转移。他们提出了一种方法来计算一个状态转移到另外一个状态所需的步数，并为之设计了一个阶段内新奇度（Episodic Curiosity, EC）模块。这里的新奇度红利就依赖于状态之间的可达性。

1. 在每一阶段开始时，智能体的阶段记忆缓存$M$为空
2. 在每一步执行后，智能体将当前的状态与记忆中的状态进行比较以决定新奇度：如果当前的状态很稀奇（也就是从记忆中的状态到达当前状态所需步数超过了某一阈值），智能体就会得到一个奖励
3. 如果新奇度红利足够高，就将当前的状态添加到阶段性记忆缓存中去（想象一下，如果所有的状态都被添加到了记忆中去，那么任意新的状态都会在一步内被添加）
4. 重复步骤1-3直至当前阶段结束

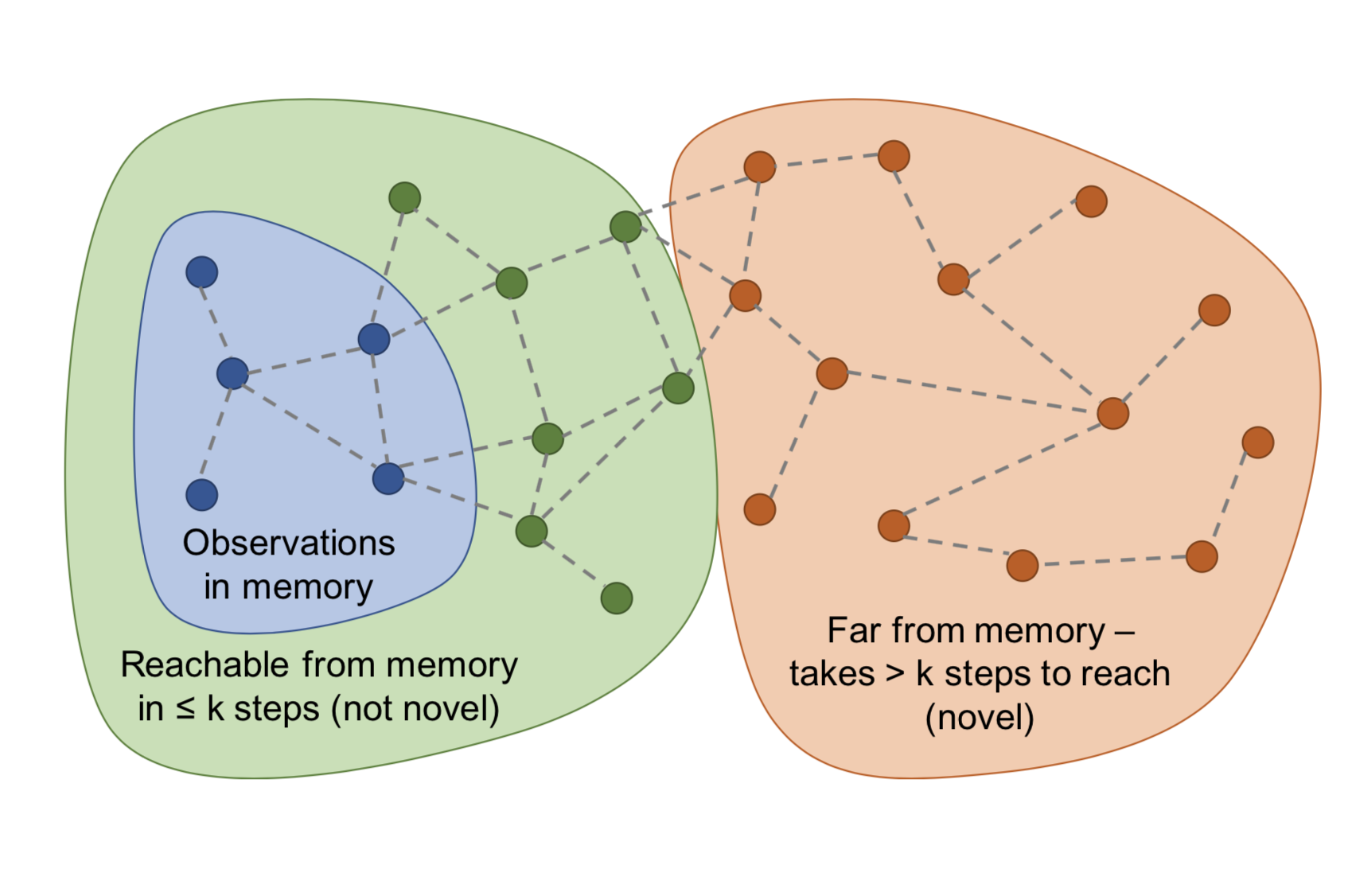
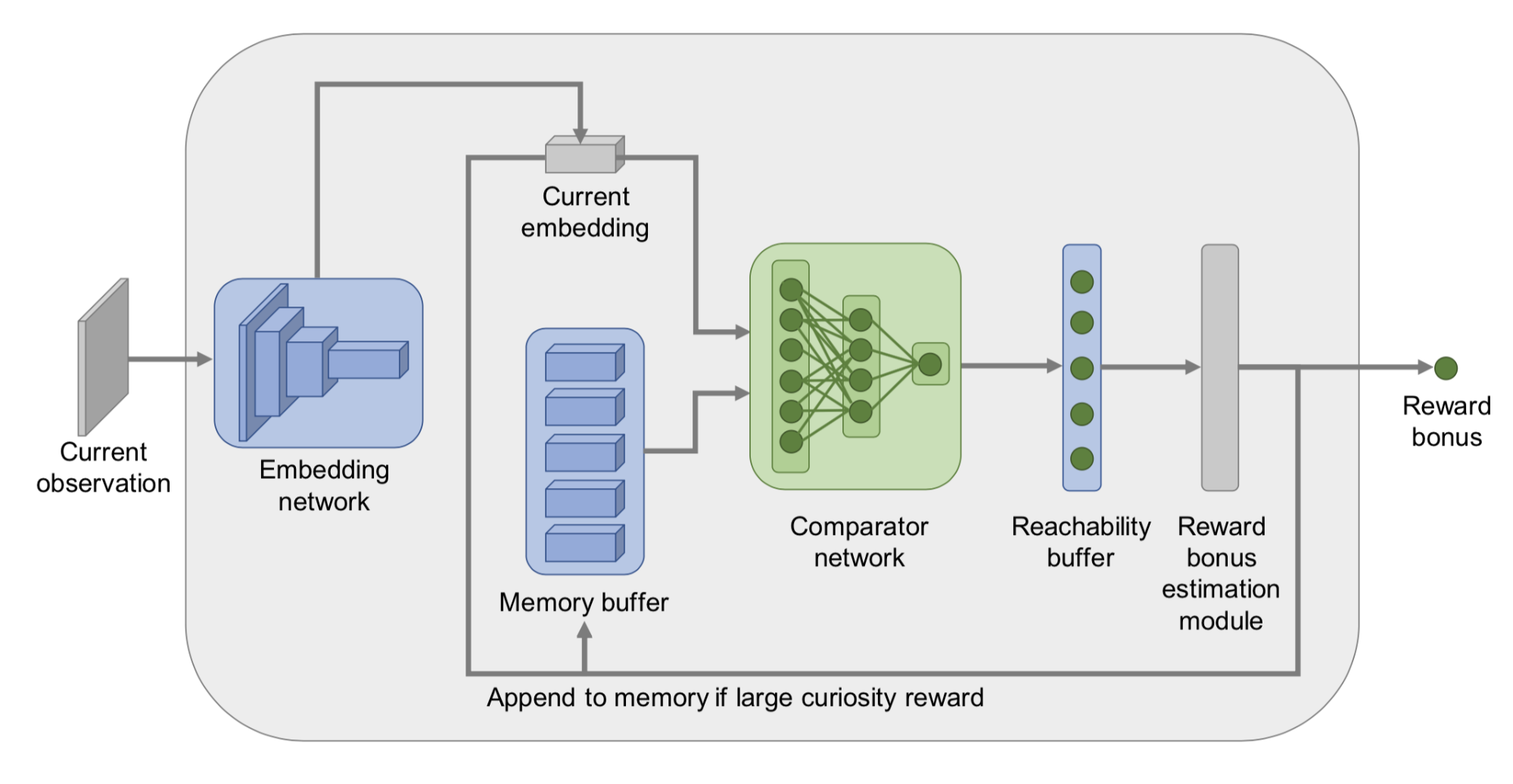
为了估计状态间的可达性，我们需要一个状态转移图，很不幸的是这个图我们并没有。在此情况下，Savinov等，2019训练了一个孪生神经网络来预测两个状态之间转移所需的步数。此网络包含了一个嵌入层$\phi: \mathcal{S} \mapsto \mathbb{R}^n$用于将状态编码为特征向量。还有一个对比网络$C: \mathbb{R}^n \times \mathbb{R}^n \mapsto [0, 1]$，它输出一个二值标签用于指示两个状态在状态图中的距离是否足够近（也就是是否$k$步可达）：$C(\phi(s_i), \phi(s_j)) \mapsto [0, 1]$。

阶段性记忆缓存中存储了同一阶段（episode）的观察（observations）的嵌入。一个新的观察会通过网络$C$与现有状态的嵌入向量进行比较，比较的结果被通过某种方式（比如：最大值、前90%等）进行聚合以得到一个可达性评分$C^M(\phi(s_t))$。最终得到的探索红利为$r^i_t = \big(C' - C^M(f(s_t))\big)$，其中$C^\prime$为一个预定义的阈值（比如在固定时间间隔的设置下，取$C^\prime$就可以工作的很好）。智能体如果访问了一个从当前记忆中的状态很难到达的一个状态，那么它就会得到一个很高的奖励。

他们声称EC模块可以解决噪声电视问题。

直接探索

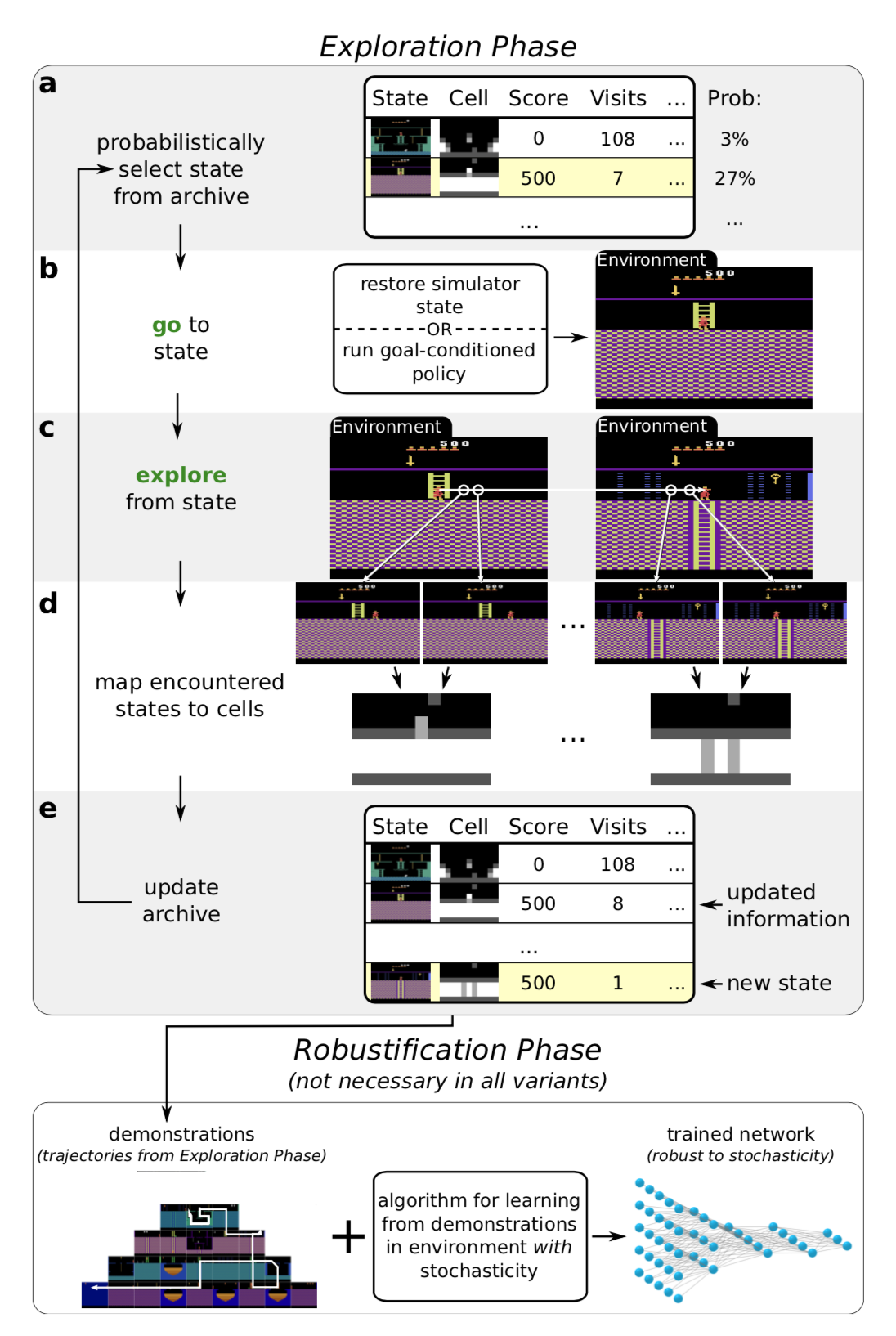
去探索（Go-Explore,Ecoffet等, 2019）算法旨在解决“硬探索”问题。它由两个阶段组成。

阶段1（"一直探索到问题解决"）感觉上与最短路径算法Dijkstra很相似。确实，在第一阶段中没有任何神经网络的影子。通过维护一个有趣状态的记忆缓存以及到达这些状态的轨迹，智能体可以返回到之前的某个状态，然后从该状态开始进行重新随机探索（需要有一个确定性的模拟器）。状态被映射到一个个短的离散码上（称作“细胞”）以便于记忆存储。记忆会在出现一个新的状态或发现一个更优的轨迹时被更新。那么如何选择返回到过去的哪一个状态呢？智能体的策略可以有多种，比如：均匀采样，使用最新访问时间、访问次数、邻居个数等数据进行启发式选择等等。这个过程会被一直重复直到任务被完成，即至少找到了一条解决方案轨迹。

上述的这种高性能的方法在泛化到带有随机性的环境中去时，不能很好地工作。因此，我们需要阶段2（“鲁棒化”）通过模仿学习来让解决方案更加鲁棒。他们选择了反向算法。在此算法中，智能体从路径最后状态的附近开始运行强化学习的优化过程。

在第一阶段中我们需要注意的是：为了返回到一个确定性的没有探索过的状态，去探索算法依赖于一个可重置的、确定性的模拟器，这是一个非常大的缺点。

为了让算法可以在存在随机性的环境中更加适用，去探索算法的一个增强版（Ecoffet等,2020）称作基于策略去探索（policy-based Go-Explore, PBGE）稍后被提出。

• PBGE不再通过原始简单的方式选择模拟器的返回状态。返回状态的选择是基于一个目标条件策略的。此策略模型的训练使用当前记忆中最优的、可以到达某个选定状态的路径。算法使用了一个自模仿学习（Self-Imitation Learning, SIL,Oh 等, 2018）损失来尽可能提取更多成功的路径
• 同时，他们发现智能体返回到之前的某一状态进行持续探索的时候，从策略中进行采样可以比随机动作工作得更好
• PBGE另外的一个改进点是将状态图片转化为细胞的粒度（译注：类似下采样）变为可调节的。这样就可以让记忆缓存不至于太大或者太小

在原始的去探索方法之后，Yijie Guo等, 2019提出了DTSIL（Diverse Trajectory-conditioned Self-Imitation Learning），此方法的思路与PBGE类似。DTSIL维护了一个在训练期间所搜集的样本的记忆，而后用它们来通过SIL方法训练一个以路径为条件的策略（trajectory-conditioned policy）。他们还根据采样期间路径最终状态的稀有程度给不同的路径排了一个优先级。

在论文Guo等, 2019中我们也可以看到相似的算法。这篇论文的主要思想是将高不确定性的目标存储在记忆中，这样智能体就可以依赖于一个目标条件策略来重复访问这些目标状态。在每一个阶段（episode）中，智能体通过抛硬币（概率0.5）的方式来决定它是采用贪心策略（基于当前训练得到的策略网络）进行探索，还是从记忆中采样目标来进行直接的探索。

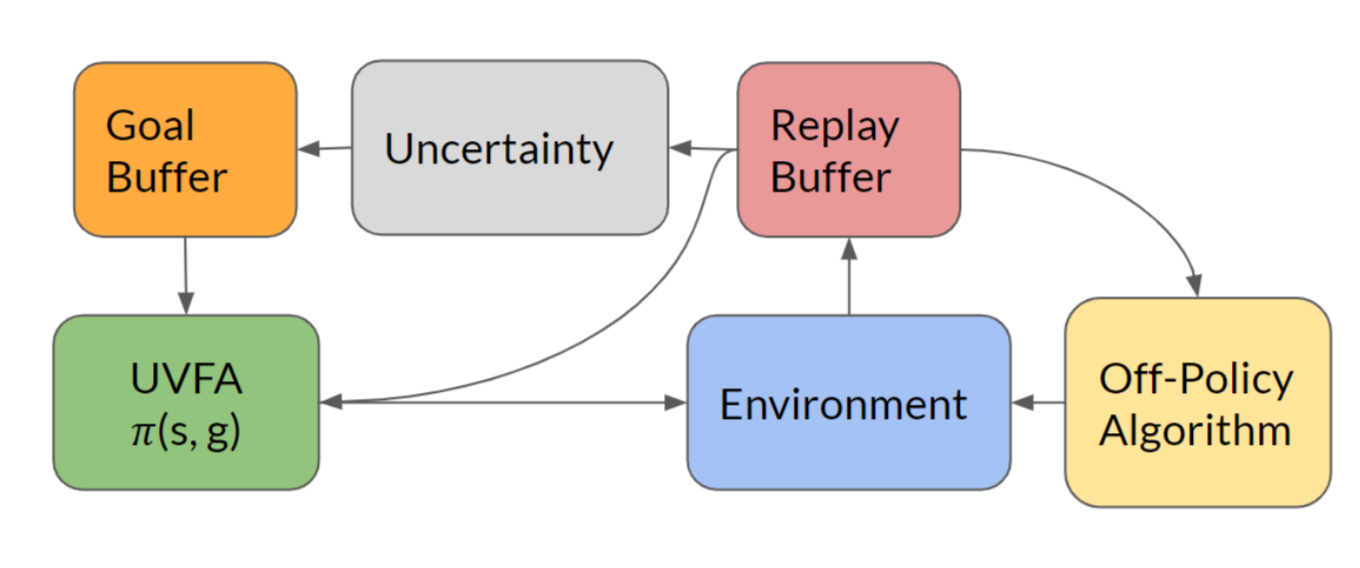
一个状态的不确定性度量可以是简单的基于计数的红利，也可以是复杂的基于密度模型、贝叶斯模型的方法。这篇论文中训练了一个前向动态模型，并以模型的预测误差作为不确定性的度量。

Q值探索

受到汤普森采样的影响，BDQN（Bootstrapped DQN,Osband等, 2016）在经典的DQN算法的基础之上，使用提升法在Q值近似上引入了一个新的不确定性概念。提升法通过从同样的样本族中进行有放回采样来近似一个分布，然后对结果进行聚合。

在训练过程中，多个Q值头部并行训练。每一个头部仅消耗数据的一个提升样本子集，并且每个都有它自己对应的目标网络。所有的Q值头部共享同样的主网络。

在每一阶段开始时，使用均匀采样得到一个Q值头部用于此阶段经验数据的搜集。而后，从一个分布$m \sim \mathcal{M}$上采样得到一个二值掩码，这些掩码被用于决定那些头部可以使用数据进行训练。掩码分布$\mathcal{M}$的选择决定了提升样本的生成方式。举例来说：

• 如果$\mathcal{M}$是一个$p=0.5$的独立二项分布，这对应着加倍提升或者不提升
• 如果$\mathcal{M}$总是返回一个值全为1的掩码，那么算法退化为聚合算法（ensemble method）

然而，由于提升算法带来的不确定性完全依赖于训练数据，此类探索仍然存在限制。更好的方式是注入一些与数据相独立的先验信息。此类“噪声”先验可以在奖励非常稀疏的时候驱动智能体持续探索。为了更好的探索（Osband等, 2018）而在BDQN中加入随机先验的算法依赖贝叶斯线性回归。贝叶斯回归算法的核心思想是：我们可以“通过对数据的带噪声版本进行训练以及一些随机正则来生成后验样本”。

令$\theta$为Q函数的参数，$\theta^-$为目标Q函数的参数。损失函数中使用了一个随机先验函数$p$：

变分选项（Varitional Options）

选项（Options,Sutton 等, 1999）是带有终止条件的策略。在搜索空间中存在着大量的选项，并且它们独立于智能体的意图（译注：这里意图应该是指一个较长期的概念，而选项是一个较短期的概念；此外，动作的影响范围一般是单步的）。通过在模型中显式地包含内在选项（intrinsic options），智能体可以获得内在探索奖励。

VIC（Variational Intrinsic Control，Gregor等, 2017）算法框架通过对选项进行建模，以选项为条件进行策略学习，为智能体提供内在探索红利。

令$\Omega$表示起于状态$s_0$终于$s_f$的选项；环境的概率分布$p^J(s_f \vert s_0, \Omega)$定义了在给定一个起始状态的情况下选项$\Omega$终于何处；可控性分布$p^C(\Omega \vert s_0)$定义了选项的采样分布。通过定义，我们有$p(s_f, \Omega \vert s_0) = p^J(s_f \vert s_0, \Omega) p^C(\Omega \vert s_0)$。

在选择选项时，我们希望达成两个目标：

• 以状态$s_0$作为起始态，获得一个丰富的最终态集合（⇨最大化$H(s_f \vert s_0)$）
• 可以精确地知道选项$\Omega$的终止于何状态（⇨最小化$H(s_f \vert s_0, \Omega)$）

将这两点组合起来，我们可以得到需要最大化的互信息：

由于互信息是对成的，我们可以在不影响等式的情况下交换几个$s_f$与$\Omega$的位置。此外，由于$p(\Omega \vert s_0, s_f)$很难被观察到，我们使用一个分布$q$来近似它。根据变分下界，我们有$I(\Omega; s_f \vert s_0) \geq I^{VB}(\Omega; s_f \vert s_0)$。

这里$\pi(a \vert \Omega, s)$可以通过任何强化学习算法来优化。选项推断函数$q(\Omega \vert s_0, s_f)$使用监督学习训练。先验$p^C$会向趋向于选择高回报的选项$\Omega$进行更新。注意这里$p^C$可以是固定的（比如一个高斯）。通过学习，不同的$\Omega$可以带来不同的行为。此外，Gregor等, 2017观察到：在实际状态下，让VIC与显式的选项一起工作非常困难。所以，他们也提出了另外一个与隐式选项一起工作的VIC。

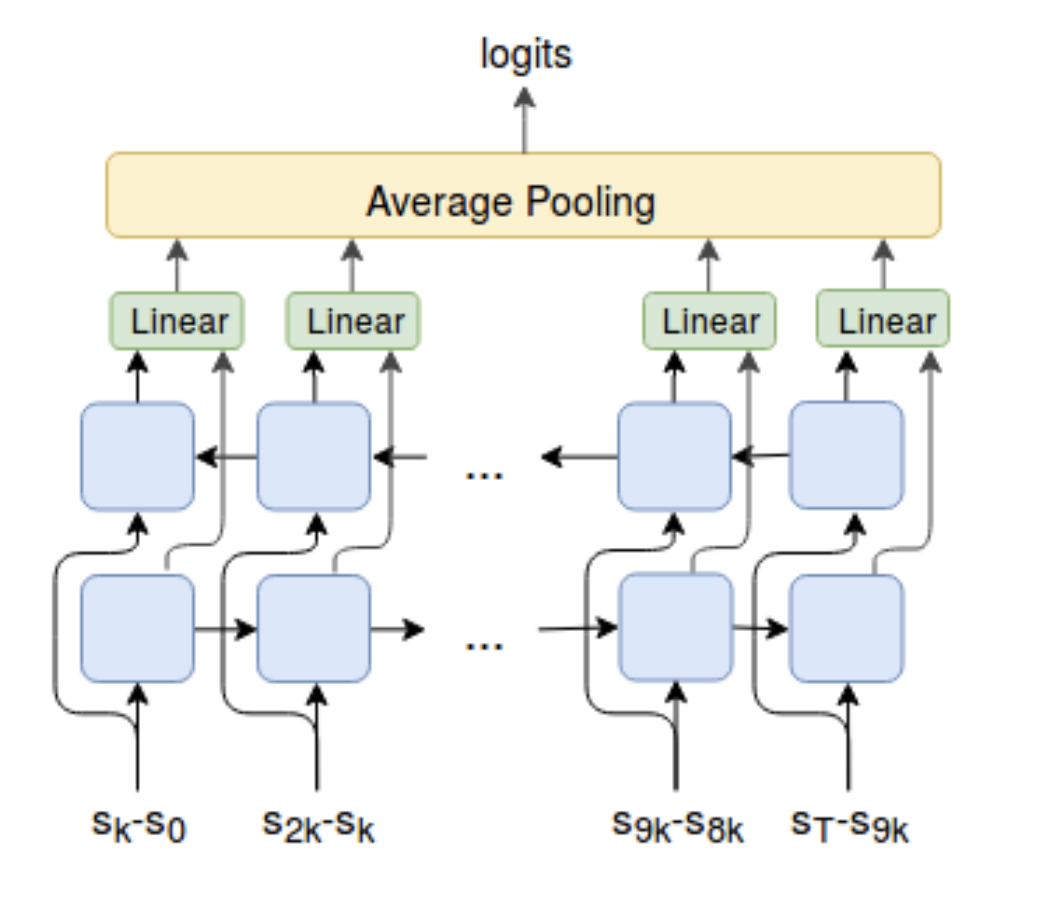
不同于仅以起始与终止态作为条件对$\Omega$进行建模的VIC，VALOR（Variational Auto-encoding Learning of Options by Reinforcement,Achiam等, 2018）依赖于整个路径来提取选项的上下文$c$（从一个固定的高斯分布中采样得到）。在VALOR中：

• 策略扮演着编码器的角色，它将从一个噪声分布中得来的上下文翻译为路径
• 解码器试图从路径中恢复上下文，并且解码器为策略提供奖励以便上下文更易于区分。编码器在训练过程中不会看到执行的动作，因此智能体与环境之间的交必须能够促进它与解码器之间进行交流，以便于预测。此外，编码器会在一个路径中反复采取一系列步骤以更好地对不同步骤之间的关系进行建模

DIAYN（Diversity Is All You Need,Eysenbach等, 2018）算法虽然名字不同，但是思路大致相同：DIAYN对策略的建模依赖于一个隐式的技巧（skill）变量。查看我之前的博文查看细节。

引用

Weng, Lilian. (Jun 2020). Exploration strategies in deep reinforcement learning. Lil’Log.https://lilianweng.github.io/posts/2020-06-07-exploration-drl/.

或者

@article{weng2020exploration,
  title   = "Exploration Strategies in Deep Reinforcement Learning",
  author  = "Weng, Lilian",
  journal = "lilianweng.github.io",
  year    = "2020",
  month   = "Jun",
  url     = "https://lilianweng.github.io/posts/2020-06-07-exploration-drl/"
}

参考文献

[1] Pierre-Yves Oudeyer & Frederic Kaplan.“How can we define intrinsic motivation?"Conf. on Epigenetic Robotics, 2008.

[2] Marc G. Bellemare, et al.“Unifying Count-Based Exploration and Intrinsic Motivation”. NIPS 2016.

[3] Georg Ostrovski, et al.“Count-Based Exploration with Neural Density Models”. PMLR 2017.

[4] Rui Zhao & Volker Tresp.“Curiosity-Driven Experience Prioritization via Density Estimation”. NIPS 2018.

[5] Haoran Tang, et al."#Exploration: A Study of Count-Based Exploration for Deep Reinforcement Learning”. NIPS 2017.

[6] Jürgen Schmidhuber.“A possibility for implementing curiosity and boredom in model-building neural controllers”1991.

[7] Pierre-Yves Oudeyer, et al.“Intrinsic Motivation Systems for Autonomous Mental Development”IEEE Transactions on Evolutionary Computation, 2007.

[8] Bradly C. Stadie, et al.“Incentivizing Exploration In Reinforcement Learning With Deep Predictive Models”. ICLR 2016.

[9] Deepak Pathak, et al.“Curiosity-driven Exploration by Self-supervised Prediction”. CVPR 2017.

[10] Yuri Burda, Harri Edwards & Deepak Pathak, et al.“Large-Scale Study of Curiosity-Driven Learning”. arXiv 1808.04355 (2018).

[11] Joshua Achiam & Shankar Sastry.“Surprise-Based Intrinsic Motivation for Deep Reinforcement Learning”NIPS 2016 Deep RL Workshop.

[12] Rein Houthooft, et al.“VIME: Variational information maximizing exploration”. NIPS 2016.

[13] Leshem Choshen, Lior Fox & Yonatan Loewenstein.“DORA the explorer: Directed outreaching reinforcement action-selection”. ICLR 2018

[14] Yuri Burda, et al.“Exploration by Random Network Distillation”ICLR 2019.

[15] OpenAI Blog:“Reinforcement Learning with Prediction-Based Rewards”Oct, 2018.

[16] Misha Denil, et al.“Learning to Perform Physics Experiments via Deep Reinforcement Learning”. ICLR 2017.

[17] Ian Osband, et al.“Deep Exploration via Bootstrapped DQN”. NIPS 2016.

[18] Ian Osband, John Aslanides & Albin Cassirer.“Randomized Prior Functions for Deep Reinforcement Learning”. NIPS 2018.

[19] Karol Gregor, Danilo Jimenez Rezende & Daan Wierstra.“Variational Intrinsic Control”. ICLR 2017.

[20] Joshua Achiam, et al.“Variational Option Discovery Algorithms”. arXiv 1807.10299 (2018).

[21] Benjamin Eysenbach, et al.“Diversity is all you need: Learning skills without a reward function.". ICLR 2019.

[22] Adrià Puigdomènech Badia, et al.“Never Give Up (NGU): Learning Directed Exploration Strategies”ICLR 2020.

[23] Adrià Puigdomènech Badia, et al.“Agent57: Outperforming the Atari Human Benchmark”. arXiv 2003.13350 (2020).

[24] DeepMind Blog:“Agent57: Outperforming the human Atari benchmark”Mar 2020.

[25] Nikolay Savinov, et al.“Episodic Curiosity through Reachability”ICLR 2019.

[26] Adrien Ecoffet, et al.“Go-Explore: a New Approach for Hard-Exploration Problems”. arXiv 1901.10995 (2019).

[27] Adrien Ecoffet, et al.“First return then explore”. arXiv 2004.12919 (2020).

[28] Junhyuk Oh, et al.“Self-Imitation Learning”. ICML 2018.

[29] Yijie Guo, et al.“Self-Imitation Learning via Trajectory-Conditioned Policy for Hard-Exploration Tasks”. arXiv 1907.10247 (2019).

[30] Zhaohan Daniel Guo & Emma Brunskill.“Directed Exploration for Reinforcement Learning”. arXiv 1906.07805 (2019).

[31] Deepak Pathak, et al.“Self-Supervised Exploration via Disagreement.”ICML 2019.

扫码关注我们：